.Quantum Leap: How Flavor Transformation Could Revolutionize Neutrino Astrophysics
http://blog.naver.com/mssoms
http://jl0620.blogspot.com
https://www.facebook.com/junggoo.lee.9
https://www.youtube.com/@SciTechDaily
.Quantum Leap: How Flavor Transformation Could Revolutionize Neutrino Astrophysics
양자 도약: 풍미 변환이 중성미자 천체물리학을 어떻게 혁명시킬 수 있을까

주제:천체물리학암사슴입자물리학인기 있는초신성 미국 에너지부 2024 년 7월 18일 양자 입자 물리학 시뮬레이션 아트 새로운 방법은 과학자들이 초신성과 중성자별 합병에서 중성미자 행동을 계산하는 방법을 단순화하여 양자적 풍미 변화를 통합하여 이러한 우주적 사건의 원소적 결과를 예측하는 유망한 도구를 제공합니다. 출처: SciTechDaily.com
연구자들은 초신성과 같은 밀도가 높은 천체물리적 환경에서 중성미자의 양자적 풍미 변화 계산을 단순화하는 방법을 개발하고 있습니다. 양자 역학을 전통적인 수송 모델에 통합함으로써 이 접근법은 항성 폭발에서 중성미자 행동과 원소 생성을 예측하는 데 도움이 되며 초기 테스트에서 유망성을 보여줍니다.
-중성미자는 "플레이버"라는 양자 역학적 속성을 가지고 있습니다 . 이 플레이버는 중성미자가 공간을 이동하면서 변형될 수 있습니다. 가장 큰 과제는 코어 붕괴 초신성 및 중성자별 합병과 같은 천체물리학 시스템에서 중성미자의 물리적 움직임과 플레이버의 변화를 모두 추적하는 것입니다. 이러한 시스템에서 복잡한 배열과 많은 수의 중성미자는 중성미자의 전부 또는 일부 하위 집합을 추적하는 것을 거의 불가능하게 만듭니다.
이 연구에서 물리학자들은 이 과제를 해결할 수 있는 잠재적인 방법을 조사했습니다. 이 접근 방식은 중성미자 이동을 계산하는 기존 방법을 확장하여 양자 역학적 풍미 변화를 포함하는 것을 포함합니다. 이 접근 방식은 복잡한 시스템에서 중성미자가 어떻게 행동하는지 계산하는 복잡성을 줄입니다.
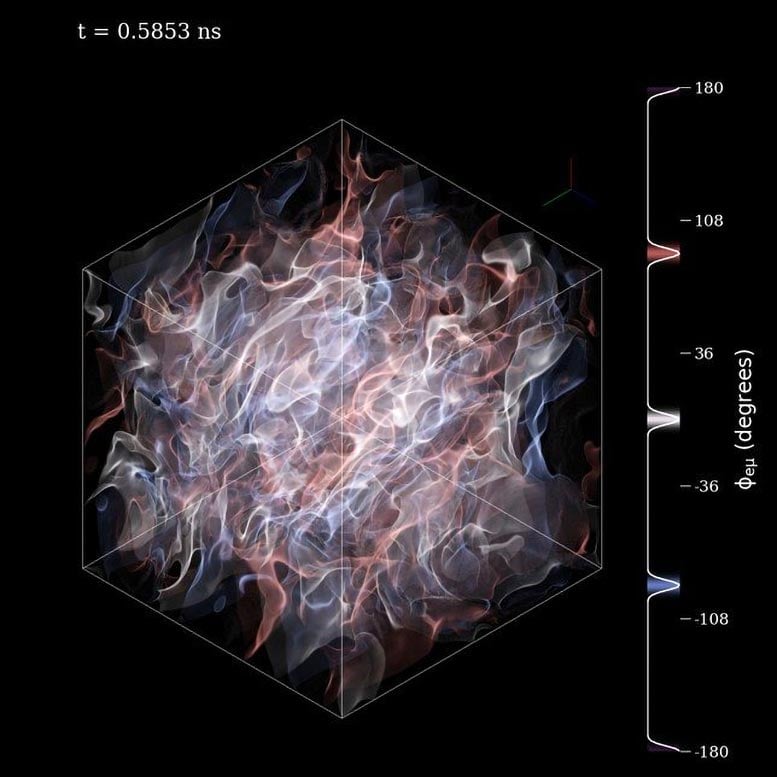
중성미자 모멘트 시뮬레이션에서 양자 코히어런스의 3D 윤곽 중성미자 모멘트 시뮬레이션에서 양자 코히어런스의 3차원 윤곽. 시뮬레이션은 무작위 초기 조건으로 시작하여 나노초 이내에 구조를 개발합니다. 출처: E. Grohs
중성미자 운동에 대한 계산 방법 확장 초신성이나 중성자별 합병은 광자 에서 중력파, 중성미자에서 중원 소에 이르기까지 다양한 유형의 메신저를 보냅니다 . 이러한 메신저는 과학자에게 이러한 항성 물체의 물리학에 대한 새로운 통찰력을 제공합니다. 그러나 과학자는 이러한 메신저를 사용하려면 중성미자 물리학을 이해해야 합니다. 중성미자는 이러한 시스템의 에너지의 상당 부분을 운반합니다. 또한 과학자들은 별의 폭발과 별의 합병에서 생성되는 중원소를 예측하기 위해 중성미자와 관련된 상호작용을 이해해야 합니다. 각 모멘트는 중성미자의 총 수와 플럭스를 작은 운동 방정식 세트로 캡슐화합니다.
그런 다음 과학자들은 이러한 방정식을 사용하여 중성미자 풍미의 변화를 계산할 수 있습니다. 각모멘트법에서 줄어든 방정식의 개수는 중성자별 합병과 같은 밀집 천체에서의 중성미자 플레이버 변환 문제를 해결하는 새로운 길을 제공합니다.
각모멘트 기반 접근 방식 테스트 이 연구에서는 중성자별 합병 잔해에서 중성미자 수송에 풍미의 양자 역학적 효과를 포함하기 위해 준고전적 각 모멘트 기반 접근법을 사용할 가능성을 조사했습니다. 연구자들은 중성미자에 대한 각 정보가 변환에 대한 알려진 요구 사항인 "빠른 풍미"라는 중성미자 풍미 변환 유형에 대해 이 방법을 테스트했습니다. 그 결과 이 방법은 변환의 성장을 잘 포착했으며 이 방법은 추가 탐색이 필요하다는 것이었습니다. 이 작업에서는 에너지부 사용자 시설인 National Energy Research Scientific Computing Center의 계산 리소스를 사용했습니다. 이 작업에서는 또한 Research Corporation for Science Advancement에서 일부 지원하는 North Carolina State University 의 Payne 머신도 사용했습니다.
참고문헌: Evan Grohs, Sherwood Richers, Sean M. Couch, Francois Foucart, James P. Kneller 및 GC McLaughlin의 "중성자별 합병을 위한 3차원 중성미자 빠른 맛 불안정성", 2023년 9월 29일, Physics Letters B. DOI : 10.1016/j.physletb.2023.138210 Evan Grohs, Sherwood Richers, Sean M. Couch, Francois Foucart, Julien Froustey, James P. Kneller 및 Gail C. McLaughlin의 "중성자별 합병에서 빠른 풍미 불안정성에 대한 응용을 통한 2-모멘트 중성미자 풍미 변환", 2024년 2월 21일, The Astrophysical Journal . DOI: 10.3847/1538-4357/ad13f2 이 연구는 주로 에너지부(DOE) 과학국, 핵물리학 프로그램에서 자금을 지원했습니다. 추가 자금은 DOE 과학국, 고급 과학 컴퓨팅 연구국, 국가 과학 재단, 하이징-시몬스 재단, 국가 항공우주청에서 지원했습니다.
mssos 메모 2407210611
msbase가 전체 집합이면 개체와 같이 시공간에서 작은 날파리처럼 고속의 선형적 움직임일 가질 수 있다. 하지만 부분집합의 형태이며 qpeoms이고 개체가 아닌 플레이버 양자 속성을 가진다.
수면의 1이 되기 위해 부분집합 상태가 그 얼마나 많은 지 물의 수면1은 온도의 변수 qpeoms.size와도 관련이 있다. 사이즈가 커지는 이유는 msoss 때문이고 임계점을 가진 사이드는 차갑고 smsbase는 커질 수록 엄청난 속도의 원회전 나선의 집단 플레이버 운동을 한다. 허허.
중성미자가 무척 작은 질점 tsp를 가지고 qpeoms=1의 임계점에 이르기 위한 플레이버 질주의 군집상태 모습은 상상하기 어렵다. 어허.

-Neutrinos have a quantum mechanical property called “flavor”. This flavor can change as neutrinos move through space. The biggest challenge is tracking both the physical movements of neutrinos and changes in their flavor in astrophysical systems such as core-collapse supernovae and neutron star mergers. The complex arrangement and large number of neutrinos in these systems make it nearly impossible to track all or some subset of neutrinos.
===========================================
mssos memo 2407210611
If msbase is the entire set, like an object, it can have high-speed linear movement like a small fly in space and time. However, it is in the form of a subset, qpeoms, and has flavor quantum properties, not entities.
Water surface 1 is also related to the temperature variable qpeoms.size. How many subset states are required to become 1 of the water surface? The reason the size increases is because of msoss, the side with the critical point is cold, and as smsbase grows, the collective flavor movement of the spiral rotates at an incredible speed. haha.
It is difficult to imagine the swarm state in which neutrinos race to reach the critical point of qpeoms=1 with a very small particle tsp. Uh huh.
Example 1.
vix.a'6//vixx.a(b1,g3,k3,o5,n6)
b0acfd|0000e0
000ac0|f00bde
0c0fab|000e0d
e00d0c|0b0fa0
f000e0|b0dac0
d0f000|cae0b0
0b000f|0ead0c
0deb00|ac000f
ced0ba|00f000
a0b00e|0dc0f0
0ace00|df000b
0f00d0|e0bc0a
sample qoms (standard)
0000000011=2,0
0000001100
0000001100
0000010010
0001100000
0101000000
0010010000
0100100000
2000000000
0010000001
sample pms (standard)
q0000000000
00q00000000
0000q000000
000000q0000
00000000q00
0000000000q
0q000000000
000q0000000
00000q00000
0000000q000
000000000q0
Sample msoss
zxdxybzyz
zxdzxezxz
xxbyyxzz
zybzzfxzy
cadccbcdc
cdbdcbdbb
xzezxdyyx
zxezybzyy
bddbcbdca
댓글