.String Theory Unravels New Pi Formula: A Quantum Leap in Mathematics

mss(magic square system)master:jk0620
http://blog.naver.com/mssoms
http://jl0620.blogspot.com
https://www.facebook.com/junggoo.lee.9

끈 이론이 새로운 Pi 공식을 밝힙니다: 수학의 비약적인 도약

$추상 수학 컨셉 아트 일러스트레이션$

주제:수학양자 물리학 인도 과학 연구소(IISC) 2024년 6월 20일 추상 수학 컨셉 아트 일러스트레이션 과학자들은 끈 이론 연구를 통해 마드하바(Madhava)의 15세기 공식을 반영하는 새로운 파이 계열을 발견했습니다. 오일러-베타 함수와 파인만 다이어그램을 결합하여 입자 상호 작용을 효율적으로 모델링했습니다. 신용: SciTechDaily.com

-연구자들은 현 이론과 입자 상호 작용을 탐구하는 동안 파이에 대한 새로운 급수 표현을 발견했습니다. 그들의 공식은 15세기 Madhava의 공식과 유사합니다. 오일러-베타 함수와 파인만 다이어그램을 결합하여 효율적인 모델을 만들어 새로운 파이 표현을 공개했습니다. 이와 같은 이론적 작업은 결국 실제 적용으로 이어질 수 있습니다. Pi의 새로운 시리즈 표현 발견 현 이론을 사용하여 특정 물리적 현상을 설명하는 방법을 조사하는 동안 인도 과학 연구소(IISc)의 과학자들은 무리수 파이에 대한 새로운 급수 표현을 우연히 발견했습니다.

이는 고에너지 입자의 양자 산란과 같은 프로세스를 해독하는 데 관련된 계산에서 파이를 추출하는 더 쉬운 방법을 제공합니다. 특정 한계 하에서의 새로운 공식은 15세기 인도 수학자 상가마그라마 마드하바(Sangamagrama Madhava)가 제안한 파이의 표현에 거의 근접하며, 이는 역사상 최초로 기록된 파이 계열이었습니다.

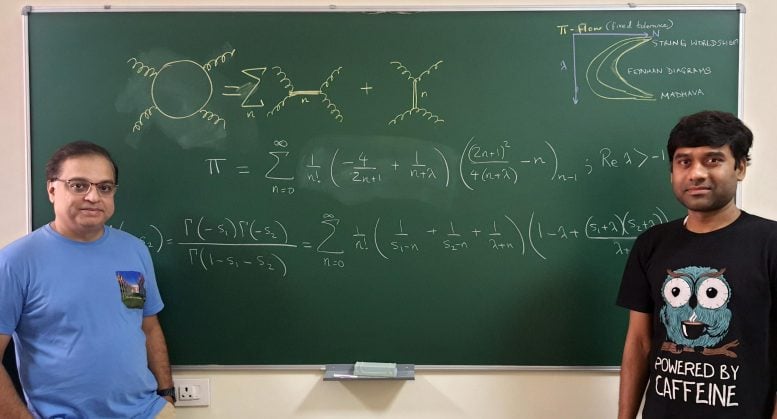
아니다 신하(Aninda Sinha)와 아르나브 사하(Arnab Saha)

이 연구는 박사후 연구원인 Arnab Saha와 고에너지 물리학 센터(CHEP)의 교수인 Aninda Sinha가 수행했으며 Physical Review Letters 에 게재되었습니다 . 아니다 신하(Aninda Sinha)와 아르나브 사하(Arnab Saha) Aninda Sinha(왼쪽)와 Arnab Saha(오른쪽). 출처: Manu Y

양자 물리학과 고에너지 입자 상호 작용 "처음에는 파이를 보는 방법을 찾는 것이 우리의 노력이 아니었습니다. 우리가 한 일은 양자 이론에서 고에너지 물리학을 연구하고 입자가 어떻게 상호 작용하는지 이해하기 위해 더 적고 더 정확한 매개변수를 가진 모델을 개발하려는 것이었습니다. 파이를 보는 새로운 방법을 얻었을 때 우리는 흥분했습니다."라고 Sinha는 말합니다. Sinha의 그룹은 끈 이론(자연의 모든 양자 과정이 단순히 끈에서 뽑아내는 다양한 진동 모드를 사용한다고 가정하는 이론적 틀)에 관심이 있습니다.

그들의 연구는 대형 강입자 충돌기에서 양성자가 서로 충돌하는 것과 같이 고에너지 입자가 서로 상호 작용하는 방식과 가능한 한 적은 수의 간단한 요소를 사용하여 이를 볼 수 있는 방법에 중점을 둡니다. 복잡한 상호작용을 표현하는 이러한 방식은 "최적화 문제" 범주에 속합니다. 움직이는 입자 각각에 대해 질량, 진동, 움직임에 사용할 수 있는 자유도 등 여러 매개변수를 고려해야 하기 때문에 이러한 프로세스를 모델링하는 것은 쉽지 않습니다. 입자 상호 작용 모델링의 과제 최적화 문제를 연구해 온 Saha는 이러한 입자 상호 작용을 효율적으로 표현하는 방법을 찾고 있었습니다.

효율적인 모델을 개발하기 위해 그와 Sinha는 오일러-베타 함수와 파인만 다이어그램이라는 두 가지 수학적 도구를 결합하기로 결정했습니다. 오일러-베타 함수는 기계 학습을 포함한 다양한 물리학 및 공학 분야의 문제를 해결하는 데 사용되는 수학 함수입니다 . 파인만 다이어그램은 두 입자가 상호작용하고 흩어지는 동안 발생하는 에너지 교환을 설명하는 수학적 표현입니다. 연구팀은 입자 상호작용을 설명할 수 있는 효율적인 모델일 뿐만 아니라, 파이의 급수 표현도 발견했습니다.

수학 급수와 파이의 빠른 계산 수학에서 급수는 파이와 같은 매개변수를 구성 요소 형태로 표현하는 데 사용됩니다. 파이가 "요리"라면 급수는 "레시피"입니다. 파이는 여러 매개변수(또는 재료)의 조합으로 표현될 수 있습니다. 파이의 정확한 값에 빠르게 근접하는 이러한 매개변수의 올바른 수와 조합을 찾는 것은 어려운 일이었습니다. Sinha와 Saha가 우연히 발견한 급수는 과학자들이 파이의 값에 빠르게 도달할 수 있도록 특정 매개변수를 결합한 다음 고에너지 입자의 산란을 해독하는 것과 같은 계산에 통합할 수 있습니다. 이론적 발견과 향후 시사점 "물리학자(및 수학자)는 적절한 도구가 없어서 지금까지 이를 놓쳤는데, 이는 지난 3년 정도 동안 협력자들과 함께 수행한 작업을 통해서만 발견할 수 있었습니다."라고 신하는 설명합니다. "1970년대 초에 과학자들은 이 연구 분야를 간략하게 조사했지만 너무 복잡해서 금세 포기했습니다."

이 발견은 현재 단계에서는 이론적이지만, 미래에 실제 응용으로 이어질 가능성이 전혀 없는 것은 아닙니다. Sinha는 Paul Dirac이 1928년에 전자의 운동과 존재에 대한 수학을 연구했지만, 나중에 그의 발견이 양전자의 발견과 질병 및 이상을 검사하는 데 사용되는 양전자 방출 단층촬영(PET)의 설계에 단서를 제공할 것이라고는 생각하지 못했다고 지적합니다. Sinha는 "이런 종류의 작업을 하는 것은 일상 생활에 바로 적용할 수 없을지 몰라도, 그저 이론을 실천하는 것 자체에 대한 순수한 즐거움을 줍니다."라고 덧붙였습니다.

참고문헌: Arnab Priya Saha와 Aninda Sinha의 "Field Theory Expansions of String Theory Amplitudes", 2024년 5월 28일, Physical Review Letters . DOI: 10.1103/PhysRevLett.132.221601

https://scitechdaily.com/string-theory-unravels-new-pi-formula-a-quantum-leap-in-mathematics/

메모 2406210421

입자들의 작은 움직임이 원원동을 한다고 가정하면 2rpi=l가 생긴다. 그 작은 입자가 선분의 양끝ab을 가진 초끈이라면 끈이 너무 짧으면 한개의 점 c(a=b)로 나타낼 수 있다. 그래서 초끈운동한다고 가정하면 3개의 꼭지점을 가진 삼각형이 나타난다. 이들이 3개의 선분으로 작아졌다 커졌다를 반복하면 초끈은 원동을 다양한 크기로 초끈입자 형태가 된다.

소스1.
양자물리학과 고에너지 입자 상호작용
“처음에 우리의 노력은 파이를 보는 방법을 찾는 것이 아니었습니다. 우리가 하고 있던 일은 양자 이론에서 고에너지 물리학을 연구하고 입자가 상호 작용하는 방식을 이해하기 위해 더 적고 더 정확한 매개변수를 사용하여 모델을 개발하려는 것뿐이었습니다. 파이를 보는 새로운 방법이 생겼을 때 우리는 매우 기뻤습니다.”라고 Sinha는 말합니다.

Sinha의 그룹은 끈 이론(자연의 모든 양자 과정이 단순히 끈에서 뽑아내는 다양한 진동 모드를 사용한다고 가정하는 이론적 틀)에 관심이 있습니다. 그들의 연구는 대형 강입자 충돌기에서 양성자가 서로 충돌하는 것과 같이 고에너지 입자가 서로 상호 작용하는 방식과 가능한 한 적은 수의 간단한 요소를 사용하여 이를 볼 수 있는 방법에 중점을 둡니다. 복잡한 상호작용을 표현하는 이러한 방식은 "최적화 문제" 범주에 속합니다. 움직이는 입자 각각에 대해 질량, 진동, 움직임에 사용할 수 있는 자유도 등 여러 매개변수를 고려해야 하기 때문에 이러한 프로세스를 모델링하는 것은 쉽지 않습니다.

1.
여기서 입자 삼각형은 xyz 각변의 초끈이 있어 susqer와 rivery 격자구조를 가진다. 이를 suri 함수로 보면 파이만의 함수처럼 양자상태의 새로운 파이계열 수식이 등장한다. 허허.
움직이는 입자 각각에 대해 질량, 진동, 움직임에 사용할 수 있는 자유도 등 여러 매개변수를 매우 정확하고 리얼하게 설명하는 나의 초끈이론 suri함수의 qpeoms.msbase.ossms 양자 물리체계의 우주를 만난다. 허허.

-Researchers discovered a new series expression for pi while exploring particle interactions with current theory. Their formula is similar to that of Madhava of the 15th century. By combining the Euler-Beta function and Feynman diagram, an efficient model was created and a new representation of pi was revealed. Theoretical work like this can eventually lead to practical applications. Discovering a new series representation for Pi While investigating how to explain certain physical phenomena using string theory, scientists at the Indian Institute of Science (IISc) stumbled upon a new series representation for the irrational number pi.

================================
Memo 2406210421

Assuming that the small movement of particles moves in a circle, 2rpi=l occurs. If the small particle is a superstring with both ends ab of the line segment, if the string is too short, it can be represented as a single point c (a=b). So, assuming super-string motion, a triangle with three vertices appears. When they repeatedly become smaller and larger into three line segments, the superstring becomes a superstring particle of various sizes.

Source 1.
Quantum physics and high-energy particle interactions
“Initially our effort was not to find a way to see the pie. All we were doing was studying high-energy physics in quantum theory and trying to develop models using fewer and more precise parameters to understand how particles interact. “We were very excited when there was a new way to look at pies,” says Sinha.

Sinha's group is interested in string theory - a theoretical framework that postulates that all quantum processes in nature use different vibrational modes that are simply plucked from strings. Their research focuses on how high-energy particles interact with each other, such as protons colliding with each other at the Large Hadron Collider, and how we can see this using as few simple elements as possible. This way of representing complex interactions falls into the category of “optimization problems.” Modeling these processes is challenging because for each moving particle, several parameters must be considered, including mass, vibration, and degrees of freedom available for movement.

One.
Here, the particle triangle has superstrings on each xyz side and has a susqer and rivery lattice structure. If you look at this as a suri function, a new pi-series formula for the quantum state appears, like pi's function. haha.
Meet the universe of the quantum physical system qpeoms.msbase.ossms of my super string theory suri function, which very accurately and realistically explains various parameters such as mass, vibration, and degrees of freedom available for movement for each moving particle. haha.

sample qoms (standard)
0000000011=2,0
0000001100
0000001100
0000010010
0001100000
0101000000
0010010000
0100100000
2000000000
0010000001

sample pms (standard)
q0000000000
00q00000000
0000q000000
000000q0000
00000000q00
0000000000q
0q000000000
000q0000000
00000q00000
0000000q000
000000000q0

Sample msoss
zxdxybzyz
zxdzxezxz
xxbyyxzz
zybzzfxzy
cadccbcdc
cdbdcbdbb
xzezxdyyx
zxezybzyy
bddbcbdca