.Cutting-edge mathematics provides new tool for particle collision puzzle
http://blog.naver.com/mssoms
http://jl0620.blogspot.com
https://www.facebook.com/junggoo.lee.9
.Cutting-edge mathematics provides new tool for particle collision puzzle
최첨단 수학은 입자 충돌 퍼즐을 위한 새로운 도구를 제공합니다

고등연구소 제공 출처: Maximilien Brice: CERN JUNE 7, 2024
-과학자들은 2012년에 처음으로 힉스 입자를 발견한 LHC(Large Hadron Collider)와 같은 입자 물리학 실험에 대한 예측을 연구하기 위해 전산 대수 기하학을 사용해 왔습니다. 새로운 수학적 도구와 결합된 이러한 실험은 물리학에서 답이 없는 문제를 훨씬 더 빠른 방법으로 해결하는 데 도움이 되며 자연에 대한 우리의 이해에 깊은 영향을 미칩니다. 팀의 결과는 3월 Physical Review Letters 에 게재되었습니다 .
-연구팀에는 자연과학부 소속인 Sebastian Mizera와 그의 협력자인 Claudia Fevola(인리아 파리-사클레 대학), Simon Telen(막스 플랑크 과학수학연구소)이 포함되어 있습니다. 이번 여름 IAS에서 5년 임기를 마무리하는 Mizera는 "우리의 발전은 최근에 개발된 전산 대수 기하학 도구를 활용 함으로써 가능해졌습니다 "라고 말했습니다. "수학의 최첨단 도구를 사용하는 것이 입자 물리학의 실제 계산에 직접적인 영향을 미치는 드문 예입니다."
-입자 충돌을 연구할 때 물리학자들은 입자가 특정 상태(예: 서로 통과하는지, 변형하는지, 다른 각도로 산란하는지)에 도달할 확률을 설명하려고 합니다. 이를 통해 새로운 입자를 식별하거나 기존 입자의 특성을 분류할 수 있습니다. 이를 위해서는 양자 수준에서 입자 상호 작용을 연구해야 합니다. 그러나 양자 이론 에서는 입자 충돌의 결과를 완전히 확실하게 예측하는 것은 불가능합니다.
-대신, 물리학자들은 입자가 상호 작용하거나 충돌할 때 발생할 수 있는 다양한 결과의 가능성을 인코딩하는 수학적 표현인 "산란 진폭"을 계산합니다. 물리학자들이 이러한 진폭에서 찾는 특징 중 하나는 확률 진폭이 무한하거나 정의되지 않는 지점 또는 영역인 "특이점"입니다.
-논문에서 Mizera와 그의 동료들은 특정 종류의 특이점, 즉 Landau 특이점을 더 잘 이해하기 위해 위상수학, 기하학, 대수학을 포함한 수학적 도구를 사용했습니다. 란다우 특이점은 가상 입자(불확정성 원리에 의해 제한되는 입자)가 관찰 가능한 입자가 될 때 정량화되는 기하학적 객체입니다. 란다우 특이점의 의미를 이해함으로써 물리학자들은 새로운 입자의 생성과 같은 새로운 현상이 가능할 수 있는 에너지 규모와 운동학 체제를 식별할 수 있습니다. 이는 실험을 해석하고 예측하는 데 중요한 역할을 합니다.
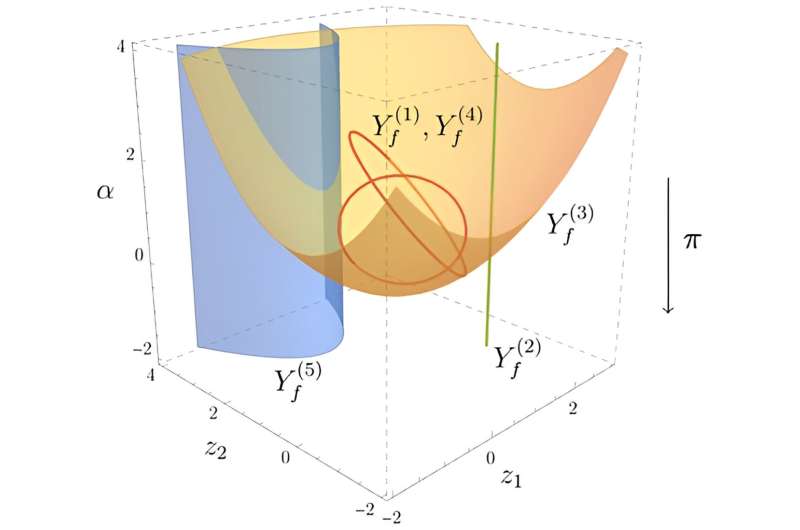
대수 방정식으로 설명되는 Landau 특이점의 표현입니다. 크레딧: 고등연구소
와 그의 동료들이 논문에서 소개한 "주요 Landau 행렬식"이라는 대수적 다양성이 이 점에서 훨씬 더 도움이 될 것 같습니다. 주요 Landau 변형은 질량이 없는 입자가 있는 경우에도 특이점을 찾습니다. 이는 매우 중요합니다.
- 질량이 없는 입자가 존재하는 상태에서 특이점을 찾는 것은 동시에 LHC의 물리학을 이해하는 데 가장 중요한 경우이자 수학적 관점에서 계산하기 가장 어려운 경우입니다. 이 능력은 강력한 핵력이 존재하는 상황에서 힉스 보손 생성을 이해하는 데 필요한 계산을 포함하여 여러 가지 예를 통해 논문에서 입증되었습니다. LHC에서 입자물리학 표준모델의 예측을 검증하는 데 사용되는 고정밀 계산 능력을 향상시키는 것은 전 세계 물리학자들의 지속적인 발전에서 중요한 단계입니다. 미제라(Mizera)와 같은 이론 물리학자들과 그의 동료들은 이 입자 퍼즐의 필수적인 부분입니다.
추가 정보: Claudia Fevola et al, Landau Singularities Revisited: Feynman 적분을 위한 전산 대수 기하학, Physical Review Letters (2024). DOI: 10.1103/PhysRevLett.132.101601 저널 정보: 실제 검토 편지 고등연구소 제공
https://phys.org/news/2024-06-edge-mathematics-tool-particle-collision.html
메모 2406102034 나의 사고실험 qpeoms 스토리텔링
질량없는 입자의 특이점은 qms.qvixer 1+1=2, 1-1=0에서 0이 질량없는 양자적 개념의 특이점이다. 2poms.zz' =1 공유점에서 입자군이 상호 작용하거나 충돌할 때 발생할 수 있는 다양한 결과의 가능성을 인코딩하는 수학적 표현인 산란 진폭을 계산한다. 이러한 진폭에서 찾는 특징 중 하나는 확률 진폭이 무한하거나 정의되지 않는 지점 또는 영역인 특이점이다.

-When studying particle collisions, physicists try to describe the probability that particles reach certain states (e.g., passing through each other, deforming, or scattering at different angles). This allows you to identify new particles or classify the properties of existing particles. This requires studying particle interactions at the quantum level. However, in quantum theory it is impossible to predict the outcome of particle collisions with complete certainty.
-Instead, physicists calculate “scattering amplitude,” a mathematical expression that encodes the likelihood of different outcomes that can occur when particles interact or collide. One of the features physicists look for in these amplitudes is a “singularity,” a point or region where the probability amplitude is infinite or undefined.
- Finding singularities in the presence of massless particles is simultaneously the most important case for understanding the physics of the LHC and the most difficult case to calculate from a mathematical point of view. This ability is demonstrated in the paper through several examples, including the calculations needed to understand the creation of the Higgs boson in the presence of the strong nuclear force. Increasing the high-precision computational power used to verify predictions of the Standard Model of particle physics at the LHC is an important step in the continued advancement of physicists around the world. Theoretical physicists like Mizera and his colleagues are an essential part of this particle puzzle.
=============================================
Memo 2406102034 My thought experiment qpeoms storytelling
The singularity of a massless particle is qms.qvixer 1+1=2, 1-1=0, where 0 is the singularity of the massless quantum concept. 2poms.zz' =1 Calculates the scattering amplitude, a mathematical expression that encodes the likelihood of different outcomes that can occur when swarms of particles interact or collide at a shared point. One of the features we look for in these amplitudes is the singularity, which is a point or region where the probability amplitude is infinite or undefined.
vix.a'6//vixx.a(b1,g3,k3,o5,n6)
b0acfd|0000e0
000ac0|f00bde
0c0fab|000e0d
e00d0c|0b0fa0
f000e0|b0dac0
d0f000|cae0b0
0b000f|0ead0c
0deb00|ac000f
ced0ba|00f000
a0b00e|0dc0f0
0ace00|df000b
0f00d0|e0bc0a
sample qoms (standard)
0000000011=2,0
0000001100
0000001100
0000010010
0001100000
0101000000
0010010000
0100100000
2000000000
0010000001
sample pms (standard)
q0000000000
00q00000000
0000q000000
000000q0000
00000000q00
0000000000q
0q000000000
000q0000000
00000q00000
0000000q000
000000000q0
Sample msoss
zxdxybzyz
zxdzxezxz
xxbyyxzz
zybzzfxzy
cadccbcdc
cdbdcbdbb
xzezxdyyx
zxezybzyy
bddbcbdca

.Peter Scholze, an unstoppable number theory pioneer who cleared away the ‘fog’ of difficult mathematics.
난해한 수학 ‘안개’ 걷어낸, 거침없는 정수론 개척자 페터 숄체
30세 ‘2018 필즈상’ 수상 페터 숄체의 수학 세계 수정 2019-10-19 20:29등록 2018-08-20 10:25 지난 8월1일 브라질 리우데자네이루에서 열린 세계수학자대회(ICM, www.icm2018.org) 개막식에서 네 명의 젊은 수학자들이 수학의 노벨상이라 불리는 ‘필즈상’을 수상했다. 오스트레일리아의 악사이 벤카테슈(Akshay Venkatesh, 36), 이탈리아의 알레시오 피갈리(Alessio Figalli, 34), 영국 국적(난민 자격)의 쿠르드인인 코체르 비르카르(Caucher Birkar, 40)와 함께 30세 수상자인 독일의 페터 숄체(Peter Scholze, 30)가 그 영예의 수상자가 됐다. 일찌감치 세계 수학계에서 ‘수상자 0순위’로 주목을 받아왔던 천재 수학자 페터 숄체의 독창적이면서도 난해한 정수론과 산술수학 분야 업적을 소개하는 글을 고등과학원의 김완수 연구원이 보내왔다.
추상적이고 난해한 수학 분야에서 이룬 숄체의 독창적인 업적을 수학에 관심을 둔 일반 독자들이 조금이나마 이해할 수 있도록 고심하며 이 글을 썼다고 한다. 좀 더 전문적인 글은 고등과학원의 웹진 ‘호라이즌’에서 볼 수 있다.
만 40세 이하의 수학자에게만 4년에 한 번씩 수여되는 필즈상은 종종 ‘수학의 노벨상’이라고 불린다. 사실 필즈상과 노벨상 사이에 직접적인 연관은 없지만, ‘노벨 수학상’이 따로 없는 만큼 수학계에서 노벨상에 견줄 만한 최고 권위의 상을 꼽아야 한다면 그것은 필즈상일 것이다. 최고 권위의 상인 만큼 수상자 발표를 앞둔 시점까지 수학계에선 이번에 누가 수상할지를 두고 여러 가지 예측이 오가기도 하지만, 이 글에서 소개하는 수상자는 이미 오래 전부터 수학계 안에서 ‘2018년 필즈상 수상 후보 0순위’로 거론되어 왔다.
사실 이번에 받지 못했다 해도 다음에 받을 것이고, 어떤 의미로는 2014년에 이미 필즈메달을 받았어도 전혀 이상하지 않았을 것이다. 이 글에서 소개할 바로 그 수학자는 2018년 필즈상 수상자 중 한 명인 독일 수학자 페터 숄체(Peter Scholze)이다. 광고 24살에 독일 역사상 최연소 수학 교수에 광고 광고 숄체는 1987년 12월 옛 동독의 드레스덴에서 태어났다. 이후 베를린에 있는 하인리히-헤르츠-김나지움이라는 수학, 과학 특성화 중고등학교에 진학하였는데, 만 14세 때 이미 수학교사가 더 이상 가르칠 것이 없으니 대신 베를린 소재 대학에서 수학 과목을 수강하라고 조언하였다.
그리고 2년이 지난 뒤 숄체는 학부 수학 과목마저 마스터하여 대학교는 그에게 지도교수를 붙여 주었고, 지도교수는 (여전히 고등학생인) 숄체에게 그로텐디크의 대수기하 이론을 지도하였다. (1966년 필즈상 수상자인 그로텐디크의 대수기하 이론은 상당히 추상적이어서 많은 대학원생들이 어려워하는 이론이기도 하다.) 다시 수년 뒤 숄체가 고등학교를 졸업하자, 당시 지도교수의 주선 하에 숄체는 본 대학에 진학하여 정수론과 산술기하의 대가인 미하엘 라포포르트 교수의 지도학생이 되었다. 본 대학에서 숄체는 학부와 석사과정을 2년 반만에 마쳤는데, 만 22세였던 2010년에 발표한 석사논문은 ‘국소 랭글랜즈 상관관계’라는 정수론의 중요한 정리를 새로운 방식으로 증명한 것으로, 이를 통해 정수론 학계에 숄체의 이름이 널리 알려지게 되었다.
그리고 2012년, 석사논문 결과보다 더 큰 센세이션을 불러일으킨 박사논문 결과로 박사 졸업 후에 곧바로 본 대학에 교수로 임용되었다. 당시 숄체는 만 24세였으며, 독일 역사상 가장 어린 나이에 교수가 되었다. 광고 외적으로 화려한 경력만큼이나 그의 연구성과도 독보적이다. 대학원생 시절의 연구성과를 보면, 기존의 방대한, 때로는 난해하고 잘 정돈되지 않은 방법론으로 증명된 결과들을 개념적으로 명료하게 이해하는 관점을 제시하는 것에서 시작하는 경우가 많다.
이렇게 문제를 둘러싼 ‘안개’를 걷어내는 순간, 기존에는 보이지 않던 길이 자연스럽게 열리며 놀라운 결과를 증명해 내는 것이다. 숄체의 예전 결과는 기존의 결과를 가장 명료하게 이해하는 관점을 제시하는 것에서 시작했다면, 최근 2-3년 간의 결과는 기존에 보이지 않던 새로운 길, 혹은 독창적인 방법론을 제시하는 것에서 시작한다. 그의 연구의 상당한 분량은 그가 새롭게 제시하는 추상적 이론의 기반을 다지는 데 할애되고, 이런 면에선 1966년 필즈상 수상자인 그로텐디크와 여러 모로 상통하는 면이 있다. 하지만 추상적인 연구 속에서도 숄체는 정수론의 구체적인 응용에 대해 꾸준히 놀라운 결과를 내고 있다. (물론 여기에서 ‘구체적인 응용’이라 함은 ‘숄체의 다른 연구와 비교할 때 구체적이다’라는 뜻으로 이해하는 것이 좋다.) 결국 ‘수학 난제의 해결’이란 측면에서만 보더라도 숄체에게 수여된 필즈상에 논란의 여지가 없겠지만, 다른 측면으로는 숄체에게 수여된 필즈상에 앞으로 그의 이론이 얼마나 발전할지에 대한 기대감이 담겨 있는 것이 아닐까 하는 생각도 든다.
국제수학자연맹(IMU) 홈페이지에 실린 숄체의 필즈상 수상 업적을 의역을 곁들여 번역하면,
(1) 퍼펙토이드 공간의 도입으로 p진수 위의 산술기하에 혁신을 불러일으켰고, (2) 이 새로운 이론을 응용하여 갈루아 표현에 관한 결과를 얻었으며, (3) 또한 새로운 코호몰로지 이론을 개발한 점 이라고 소개되어 있다.(이쯤에서 숄체의 업적을 일반 독자들에게 소개해야 하는 필자의 고뇌를 느낄 수 있을지 모르겠다.)
먼저 여기에 언급된 업적 중에서 가장 근원이 되는 업적은 숄체가 2011년 박사 논문연구의 일환으로 도입한 ‘퍼펙토이드 공간’이라는 개념이다. 여기에 언급된 다른 업적들은 ‘퍼펙토이드 공간 이론’의 기반 위에 설립된 결과들이다. 하지만 이 개념을 정수론 이외의 분야를 연구하는 수학자에게 설명하는 것조차 쉽지 않으며, 또한 왜 이 이론을 통해 숄체를 포함한 많은 수학자들이 놀라운 결과를 증명해낼 수 있는지 대중에게 설명하는 것은 쉽지 않다. 그래서 이 글에서는 아쉽게도 퍼펙토이드 공간에 대한 설명은 생략하고, 위에서 두 번째로 언급된 “갈루아 표현에 관한 결과”에 대해서만 집중하도록 하겠다. 디오판토스 방정식: 정수론의 근원 정수론은 수학의 가장 오래된 분야 중 하나이다. 정수는 가장 ‘기본적인 수’이기에, 아마도 고대부터 정수의 성질을 연구해 왔을 것이다. 그중에도 역사적으로 오래 된 문제는 방정식의 정수해를 구하는, 소위 ‘디오판토스 방정식’ 문제이다. ‘디오판토스 방정식’이란 이름은 방정식의 정수해를 구하는 문제와 해법이 기원후 3세기 그리스 수학자인 디오판토스에 의해 집대성되었기 때문에 붙여진 것이다. 위키피디아의 ‘정수론’ 페이지에 따르면, 현존하는 가장 오래된 정수론 문헌은 기원전 1800년 경에 메소포타미아에서 작성된 점토판 ‘플림프턴 322(Plimpton 322)’라고 한다. 이 점토판에 기록된 숫자들은 직각삼각형 세 변의 길이를 이루는 정수의 쌍이라는 이론이 중론인 듯하다. 시간의 여유가 있다면 중학교 수학 시간에 배운 ‘피타고라스 정리’의 기억을 되살려서 세 변의 길이가 모두 정수인 직각삼각형을 5개만이라도 찾아보자. 인터넷을 찾지 않고 조금만 시도해 본다면 직각삼각형의 세 변의 길이를 모두 정수로 맞추는 것이 결코 쉽지 않다는 점을 깨닫게 될 것이다. 만약 직각을 낀 두 변의 길이를 1로 한다면 피타고라스의 정리에 의해 빗변의 길이는 √2가 되어 정수가 아니게 된다. 만약 직각을 낀 두 변의 길이를 1과 2로 한다면 빗변의 길이는 √5 가 되어 여전히 정수가 아니게 된다. 직각삼각형의 변의 길이를 주는 정수의 쌍을 8개만 적어 보면 아래와 같다.
(3, 4, 5), (5, 12, 13), (8, 15, 17), (7, 24, 25), (20, 21, 29), (12, 35, 37), (9, 40, 41), (28, 45, 53), ...
숫자가 커지면서 복잡해짐을 한눈에 확인할 수 있다. 피타고라스 정리를 잠시 복습하면, 직각을 낀 변의 길이를 x와 y로 놓고, 빗변의 길이를 z라고 놓았을 때 x, y, z는 아래와 같은 이차방정식을 만족한다.
직각삼각형의 변의 길이를 주는 정수의 쌍이란 다름이 아닌 위 이차방정식의 정수해이다. 즉 일반적으로는 방정식의 실수해를 찾는 것보다 정수해를 찾는 것이 훨씬 복잡하다는 점을 이 예시를 통해 알 수 있다. 이제 근대로 넘어와서, 17세기 프랑스 수학자인 피에르 드 페르마는 3 이상의 정수인 n에 대해서 xⁿ + yⁿ = zⁿ이 양의 정수해를 가질 수 없음을 증명했다고 주장하였으나, 그 증명은 남기지 않았다. 즉 아래와 같은 방정식을 만족하는 양의 정수 x, y, z가 존재하지 않다고 주장한 것이다.
이 ‘주장’은 ‘페르마의 마지막 정리’라는 이름이 붙여졌고, 페르마의 마지막 정리를 증명하는 것은 오랫동안 정수론의 대표적인 난제로 남아 있었다. 19세기 수학자 에른스트 쿰머는 페르마의 마지막 정리의 일부 경우를 증명하였고, 여기에 사용된 이론은 정수론의 다른 분야에도 응용되면서 현대의 대수적 정수론의 토대를 형성하게 된다. 그리고 약 1세기 반이 지난 1994년, 앤드류 와일즈가 페르마의 마지막 정리의 완전한 증명을 발표하였다. 와일즈의 증명은 ‘랭글랜즈 프로그램’이라고 지칭되는 상당히 복잡하고 추상적인 가설의 일부를 해소하는 것을 통해 페르마의 마지막 정리를 증명한 것이다. 와일즈의 연구를 시발점으로 랭글랜즈 프로그램에도 놀라운 진전이 있었고, 어떤 의미에선 와일즈의 증명이 정수론에 끼친 임팩트는 페르마의 마지막 정리를 증명한 것보다는 랭글랜즈 프로그램에 돌파구를 연 것에 있다고 해도 좋을 것이다.
다시 방정식의 정수해를 구하는, 즉 ’디오판토스 방정식’을 푸는 문제로 돌아오자. 운이 좋다면 방정식의 정수해를 찾을 수 있고, 심지어는 모든 정수해를 찾는 알고리즘을 찾을 수도 있다.(앞에서 언급한 x² + y² = z²이 그런 예이다.) 하지만 방정식의 모양을 조금만 바꾸면 정수해를 구하는 문제가 전혀 달라지거나 극단적으로 어려워지기도 한다.(페르마의 마지막 정리가 그런 예이다.) 어떤 방정식의 경우에는 정수해를 구하는 문제가 별다른 이론 없이 단순히 영리한 트릭으로 해결되는 경우도 있는가 하면, 페르마의 마지막 정리처럼 방정식을 풀기 위해 예상치 못하게 매우 깊은 이론이 필요한 경우도 있다. 그리고 방정식의 정수해는 자명하게 보이지 않는 한 존재성을 판별하는 것이 일반적으로 매우 어려울 수도 있다.
사실 주어진 방정식의 정수해 유무를 감별하는 알고리즘이 존재할 수 없다는 정리가 1970년 유리 마티야세비치에 의해 증명된 바 있다. 어떤 의미로는 방정식의 정수해를 푸는 문제는 많이 연구되어 있는 경우를 제외하면 ‘복불복’의 성격이 짙다. 그래서 대수적 정수론은 이 문제에 조금 다르게 접근한다. 단순히 말하자면 발상을 전환하여 문제를 조금 바꾸는 것이다. 발상의 전환: 갈루아 이론 예를 들기 위해 앞에서 언급한 방정식 x³ + y³ = z³을 살펴보자. 페르마의 마지막 정리에 의해 어떤 양의 정수 x, y, z도 이 방정식을 만족할 수 없다. (사실 이 경우는 18세기 오일러 등에 의해 이미 알려져 있었다.) 하지만 양의 정수해에 집착하는 대신 조금 일반적인 해를 생각하면 방정식을 풀 수 있는 방법이 많이 있다.
예를 들면, x³ + y³ = z³을 만족한다. (다만 ³√2이 정수가 아닐 뿐이다.) 19세기 대수적 정수론의 ‘발상의 전환’은 정수해만 생각하는 대신 조금 더 일반적인 방정식의 해를 생각한 다음 그들 사이의 ‘대칭’을 연구하는 것이다. 비록 제한적인 경우이긴 하지만 이런 발상의 전환이 방정식의 정수해를 찾는 문제에 응용되기도 한다.(앞에서 언급한 쿰머의 페르마 마지막 정리의 부분증명이 이런 접근법에 해당한다.) 그리고 이외에도 정수론의 많은 문제들은 결국 방정식의 해의 대칭에 관한 문제로 귀결된다. 방정식 해의 대칭이 중요하다는 발상은 19세기 초 비운의 천재 수학자 에바리스트 갈루아에 의해 처음 등장하였다. 그는 해의 대칭을 연구하는 것을 통해 오차 이상의 일변수 방정식에 일반적으로 적용되는 ‘근의 공식’이 존재할 수 없음을 보였고, 그 이후 해의 대칭에 관한 이론을 통상적으로 ‘갈루아 이론’이라고 부른다. 간단한 예시 이제 갈루아 이론에서 말하는 ‘해의 대칭’의 간단한 예를 들어 보고자 한다. 먼저 방정식을 생각해 보자. 변수 x에 정수들을 대입해 보면 이 방정식의 정수해가 없음은 쉽게 알 수 있다. 다만 정수에 국한하지 않고 해를 찾아보면, 먼저 x = √2라는 해를 찾을 수 있다. 그리고 조금 생각해 보면 x = -√2 역시 위 방정식을 만족하며, 두 개의 해 √2와 -√2 사이에는 부호를 바꾸는 대칭이 있다. (‘해의 대칭’은 일반적으로는 해를 무작위로 섞는 것을 의미하지 않고 추가로 만족해야 하는 성질이 있지만, 지금 고려하고 있는 방정식 x² = 2의 경우에는 두 개의 해를 뒤바꾸는 것이 해의 대칭을 준다.)
랭글랜즈, 와일즈, 그리고 숄체 대수적 정수론의 문제들은 임의의 방정식에서 얻어지는 해의 대칭을 이해하는 것으로 귀결된다. 하지만 무한히 많은 방정식에서 얻어지는 해의 대칭을 모두 나열하는 것을 통해 이해하는 것은 불가능한 일이다.(오차다항식만 하더라도 해의 대칭이 아주 복잡할 수 있는데, 다항식의 차수를 무한히 올려가면서 무한히 많은 다항식을 하나씩 각개격파 하면서 전체를 이해하기는 불가능할 것이다.) 결국 갈루아 이론에서 말하는 방정식의 해의 대칭을 이해하기 위한 실현 가능한 방법은, 수학적 이론을 통해 다른 수학적 개체와 어떤 ‘상관관계’를 만드는 것이다.
1960년대 랭글랜즈는 이런 ‘상관관계’에 대해 정확한 가설을 만들기 시작하였고, 이 가설과 아이디어가 후일에 ‘랭글랜즈 프로그램’이라고 불리게 된다. 다만 방정식의 해의 대칭과 상호관계에 있는 개체가 무엇인지를 설명하는 것도 그리 쉽지 않고 상관관계의 의미도 설명하기 쉽지 않기에, 이 글에서는 자세한 설명을 생략한다. 랭글랜즈 프로그램에 관한 결과는 항상 기술적으로 복잡하고 정수론의 전문가들조차 이해하기 어려워하는 경우도 많으며, 또한 조그마한 진전을 얻기 위해서 엄청나게 어려운 노력을 해야 하는 것이 대부분이다. 하지만 랭글랜즈 프로그램을 일부라도 실현하는 결과를 얻게 되는 경우, 정수론에 어마어마한 진전을 가져다준다.
대표적인 예로 와일즈가 페르마의 마지막 정리를 랭글랜즈 프로그램의 일부를 실현하는 것으로 증명한 것이다. 물론 아직 랭글랜즈 프로그램의 완전한 실현과는 거리가 멀지만, 와일즈 이후 약 20여 년 동안 랭글랜즈 프로그램에는 커다란 진전이 있었다. 숄체는 만 16세였을 때 와일즈의 페르마 마지막 정리를 처음 접했다. 당시에는 와일즈의 증명을 전혀 이해할 수는 없었지만 깊이 매혹되었고, 와일즈의 증명을 이해하기 위한 배경 지식을 공부하기 시작하였다. 그리고 2010년 만 22세에 숄체의 이름을 정수론 학계에 널리 알린 석사논문은 랭글랜즈 프로그램에 관한 결과였고, 그 이후에도 숄체는 그의 박사논문 연구에서 개발한 ‘퍼펙토이드 공간’ 이론을 기반으로 하여 랭글랜즈 프로그램에서 가장 독보적인 결과를 내고 있다. 숄체의 필즈상 수상의 주요 업적 중 하나가 바로 랭글랜즈 프로그램에 대한 일련의 놀라운 결과들이다. 갈루아 이론의 기하적 직관 숄체는 2014년 가을 버클리에서 특별 학기 강연을 진행하면서 갈루아 이론 및 랭글랜즈 프로그램의 새로운 방향을 제시했다.
이 때 제시한 연구의 청사진은 아직 연구논문의 형태로 출판되지는 않았지만, 그 아이디어는 이미 전문가들 사이에 널리 퍼져 있으면서 해당 분야의 연구에 이미 큰 영향을 주고 있다. 조금 애매모호할지 모르지만 개략적으로 말하자면 숄체의 프로그램의 시작점은 다음과 같은 관찰이다. 관찰: 갈루아 이론, 즉 방정식의 해의 대칭은 ‘기하학적 공간’ 대칭과 많이 닮아 있다. 사실 ‘대칭’이라는 현상은 대수학이나 정수론보다는 기하학에 좀 더 친숙한 개념이다. (초등학교 때부터 그림을 통해 도형이나 그래프의 ‘대칭’을 접했을 것이다.) 그리고 어떤 측면에서는 갈루아가 탐구한 ‘해의 대칭’ 역시 19세기에 등장한 기하학의 일종인 ‘위상수학’에서 다루는 대칭과 개념적 유사성이 있다. 지금부터 비록 직접적인 수학적인 연관성은 없지만 갈루아 이론에서의 ‘해의 대칭’과 개념적으로 상당히 유사한 기하적 모델을 설명하고자 한다.
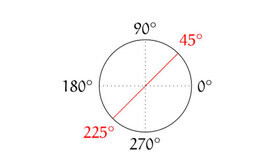
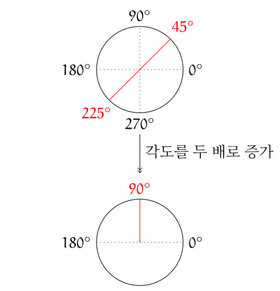
먼저 반경 1인 원을 생각해보자. 그러면 원 위의 각 점은 ‘각도’로 표기할 수 있다. 예를 들면 아래 그림에서 검은 점선과 원이 만나는 점은 중심에서 0˚, 90˚, 180˚, 270˚의 각도에 위치한 점이다. 또한 45˚와 225˚에 위치한 점 역시 표시되어 있다. 이제 원 위의 각 점의 각도를 두 배로 바꾸어서 옮겨보자. 즉 0˚에 있던 점은 그대로 그 자리에 있게 되고, 45˚에 있던 점은 90˚로, 90˚에 있던 점은 180˚로 옮기는 것이다. 아래 그림을 참고하기 바란다. 참고로 180˚에 있던 점은 360˚에 있는 점으로 겨지게 되는데, 360˚ 회전하게 되면 0˚로 돌아오게 된다. 즉 0˚와 180˚에 있던 점은 0˚로 옮겨지게 되고, 비슷한 이유로 45˚와 225˚에 있던 점은 90˚로 옮겨지게 된다.
-즉 원 위의 각 점의 각도를 두 배로 증가시켜 옮기게 되면 같은 원의 모든 점을 정확히 두 번 덮을 수 있게 된다. 여기에서 한 가지 대칭을 발견할 수 있다. 즉 원 위의 각 점의 각도를 두 배로 바꾸는 것과, 원을 먼저 180˚ 회전한 후 각 점의 각도를 두 배 바꾸는 것이 같은 결과를 준다는 점이다. 예를 들면 45˚에 위치한 점은 180˚ 회전하게 되면 225˚의 위치로 옮겨지고, 이제 각도를 두 배로 바꾸면 450˚의 위치로 가게 되는데 450˚ = 360˚ + 90˚이기 때문에 결국 90˚의 위치로 가게 된다. (아래 그림에는 파란 점선으로 180˚ 회전을 도식화하였다.)
이제 예전에 언급했던 방정식 x² = 2의 예시를 다시 생각하면, √2와 -√2를 바꾸는 ‘해의 대칭’과 위에 설명한 원을 180˚ 회전하는 변환과 개념적인 유사성이 있다고 주장하고 싶다. (물론 직접적인 수학적 연관성을 주장하는 것은 아니다.) 이 유사성을 표로 정리하자면 아래와 같다. 한 가지 첨언하고 싶은 내용은, 이차방정식의 해의 대칭은 충분히 단순하기 때문에 원의 대칭과 유사성을 가지지만, 일반적으로 고차방정식의 해의 대칭을 설명하기에는 원이라는 공간이 충분히 복잡하지 않다는 점이다. 일례로 오차방정식 x⁵ - x - 1 = 0 의 해는 120가지의 복잡한 대칭을 갖고 있지만, 원이라는 공간으로 이런 복잡한 대칭을 구현할 수 없다. 아마도 복잡한 대칭을 갖는 고차다항식의 해의 대칭과 비슷한 기하적 성질을 갖는 공간이 있다면, 원보다 훨씬 복잡할 것이다.
갈루아 이론의 기하적 구현? 지금까지의 내용을 요약하자면, 정수론의 많은 문제들인 방정식의 해의 대칭에 관한 문제로 귀결된다. 또한 방정식의 해 사이의 대칭은 어떤 종류의 ‘공간의 대칭’과 유사성이 있어 보인다. 다만 위에서 설명한 기하학적인 모델들은 갈루아 이론과 직접적인 연관이 없으며, 단지 갈루아 이론에의 직관을 얻는 데 도움을 주기 위한 도구 정도로 생각할 수 있다. 여기에서 잠깐 몽상에 가까운 질문을 하나 하자. 질문: 갈루아 이론, 즉 방정식의 해의 대칭을 기하학적으로 구현하는 ‘공간’을 만들 수 있을까? 이 질문은 단순한 개념적 유사성에 대한 것이 이니다, 위의 질문에 등장하는 ‘공간’은 단순히 갈루아 이론에 직관을 주는 도구가 아니라, 이 ‘공간’을 기하학적으로 연구하면서 갈루아 이론에 대해 자명하지 않은 결과들을 증명할 수 있어야 한다.
예를 들면 랭글랜즈 프로그램에 대한 결과를 얻어낼 수 있으면 좋을 것이다. 여기에 숄체가 개발한 이론의 놀라운 응용이 등장한다. 정수 혹은 유리수 위의 갈루아 이론 대신 2진수의 갈루아 이론을 생각한다면, 숄체가 2011년에 도입한 퍼펙토이드 공간의 이론을 사용하여 2진수의 갈루아 이론을 구현하는 ‘공간’을 만들어낼 수 있다는 것이다. 또한 2 대신 3, 5, 7, 11 등의 다른 ‘소수’를 사용하여도 같은 결과를 얻을 수 있다.
현재 숄체는 이러한 새로운 기하학적인 공간을 응용하여 랭글랜즈 프로그램에 대한 놀라운 결과를 증명하고 있으며, 그의 국제수학자대회 기조강연 강의록에 개략적인 아이디어가 소개되어 있다. 맺음말 리오에서 열린 2018년 국제수학자대회에서, 숄체는 필즈상 수상자의 자격으로 수많은 청중 앞에서 그의 이론을 강의했다. 필자는 이번 국제수학자대회에 참석하지는 않았지만, 작년 겨울에 미리 공개된 강의록을 공부했기에 국제수학자대회 홈페이지의 기사를 통해 숄체의 강의 내용을 어느 정도 유추할 수 있었다. 수상자 강연에서 필자가 특히 경탄한 부분은 단순히 자신이 과거에 낸 업적을 설명하는 데 만족하지 않고, 자신의 이론이 미래에 어떻게 전개되고 응용될지에 대한 방향성을 제시하는 대담하고도 놀라운 추측들을 설명한 점이다.
필즈상 수상자 중에서는 수상 이후에 필즈상 수상 업적에 걸맞는 연구성과를 내지 못하는 경우가 적지 않다. 하지만 숄체의 경우에는 필즈상 수상이 어쩌면 앞으로 숄체가 이룩할 더 위대한 업적의 ‘시작’에 불과한 것이 아닐까 라는 생각이 든다. 김완수 고등과학원 연구원 이 글을 쓴 김완수는 고등과학원 수학부에 연구원으로 재직 중이며, p진 산술기하와 코호몰로지 이론을 주로 연구하고 있다.
https://www.hani.co.kr/arti/science/science_general/858323.html#cb
메모 2406110524
대통일장이론처럼 수학에서의 대통합이론은 단일 프로젝트로 랭글랜즈 프로그램이 있다. 그런 대통합적인 한점이 수직선상에 임의점에 데데킨드절단에서 qpeoms의 대각선 꼭지점에 모인 것을 어제 확인하였다. 허허.
2018년 필즈상 수상자 숄체가 고등학교를 졸업하자, 당시 지도교수의 주선 하에 숄체는 본 대학에서 숄체는 학부와 석사과정을 2년 반만에 마쳤는데, 만 22세였던 2010년에 발표한 석사논문은 ‘국소 랭글랜즈 상관관계’라는 정수론의 중요한 정리를 새로운 방식으로 증명한 것으로, 이를 통해 정수론 학계에 숄체의 이름이 널리 알려지게 되었다.
표현론과 대수적 수론에서 랭글랜즈 프로그램(영어: Langlands program)은 로버트 랭글랜즈가 제안한 수론과 기하학 사이의 연결에 대한 광범위하고 영향력 있는 추측 구조이다. 대수적 정수론에서 갈루아 군을 국소체와 아델에 걸쳐 대수군의 보형 형식 및 표현론과 연결하려 한다.
소스1.
특히 갈루아 이론, 즉 방정식의 해의 대칭은 ‘기하학적 공간’ 대칭과 많이 닮아 있다.
사실 ‘대칭’이라는 현상은 대수학이나 정수론보다는 기하학에 좀 더 친숙한 개념이다. 어떤 측면에서는 갈루아가 탐구한 ‘해의 대칭’ 역시 19세기에 등장한 기하학의 일종인 ‘위상수학’에서 다루는 대칭과 개념적 유사성이 있다.
-원 위의 각 점의 각도를 두 배로 증가시켜 옮기게 되면 같은 원의 모든 점을 정확히 두 번 덮을 수 있게 된다. 여기에서 한 가지 대칭을 발견할 수 있다. 즉 원 위의 각 점의 각도를 두 배로 바꾸는 것과, 원을 먼저 180˚ 회전한 후 각 점의 각도를 두 배 바꾸는 것이 같은 결과를 준다는 점이다. 예를 들면 45˚에 위치한 점은 180˚ 회전하게 되면 225˚의 위치로 옮겨지고, 이제 각도를 두 배로 바꾸면 450˚의 위치로 가게 되는데 450˚ = 360˚ + 90˚이기 때문에 결국 90˚의 위치로 가게 된다.
각도를 21배로 증가
1.
원이나 구체 위 표면에는 임의점들이 무수히 있다. 이들 점들이 qpeoms=1,2 이라 가정하여 보자. 특히 zz'line.value이면 원이나 구체의 반지름 1, 2의 값이다. 이들이 무수한 임의점 a들에서 180도 각운동으로 a' 위치점을 하나더 얻었다면 a와 a'의 각운동 2배가 동일하게 a와 a'로 연결된 지름의 중앙에서 반지름의 수직선에서 y반지름 대칭으로 만난다. 이를 x^2=2의 루트값이 두개의 서로 다른 부호이지만 결국의 대칭으로 만나면, 하나의 반지름처럼 보이는 측면에서는 갈루아가 탐구한 ‘해의 대칭’ 역시 19세기에 등장한 기하학의 일종인 ‘위상수학’에서 다루는 대칭과 개념적 유사성이 있다.
그런 의미에서 대통합적인 한점이 수직선상에 임의점에 데데킨드절단에서 qpeoms의 대각선 꼭지점에 모인 것은 수학이나 물리의 대통합이론도 결국은 '한곳에 qpeoms.zz'.vixer,qvixer 모인다'는 함의일 수 있다. 허허.

Memo 2406110524
Like the Grand Unified Field Theory, the Grand Unified Theory in mathematics is a single project called the Langlands Program. Yesterday, it was confirmed that such a grand integrated point was gathered at a random point on the vertical line and at the diagonal vertex of qpeoms in the Dedekind cut. haha.
When 2018 Fields Medal winner Scholze graduated from high school, under the arrangement of his advisor at the time, Scholze completed his undergraduate and master's studies at this university in two and a half years. The master's thesis published in 2010, when he was 22 years old, was titled 'Topical He proved an important theorem of number theory called 'Langlands correlation' in a new way, and through this, Scholze's name became widely known in number theory circles.
In representation theory and algebraic number theory, the Langlands program (English: Langlands program) is a widespread and influential speculative structure on the connection between number theory and geometry proposed by Robert Langlands. In algebraic number theory, we try to connect the Galois group with the complementary forms and expression theory of algebraic groups across local bodies and Adel.
Source 1.
In particular, Galois theory, that is, the symmetry of solutions to equations, is very similar to the symmetry of ‘geometric space’.
In fact, the phenomenon of ‘symmetry’ is a more familiar concept in geometry than in algebra or number theory. In some respects, the ‘symmetry of the solution’ explored by Galois also has conceptual similarities with the symmetry dealt with in ‘topology’, a type of geometry that appeared in the 19th century.
-If you double the angle of each point on the circle and move it, you can cover all points on the same circle exactly twice. One symmetry can be found here. In other words, doubling the angle of each point on a circle gives the same result as rotating the circle 180° and then doubling the angle of each point. For example, a point located at 45˚ will be moved to a position of 225˚ if it is rotated 180˚, and now if the angle is doubled, it will be moved to a position of 450˚. Since 450˚ = 360˚ + 90˚, it will eventually be moved to a position of 90˚. will go to
Increase angle by 21 times
One.
There are countless random points on the surface of a circle or sphere. Let's assume that these points are qpeoms=1,2. In particular, zz'line.value is the value of the radius 1 or 2 of a circle or sphere. If they obtain one more location point a' through 180-degree angular movement from countless random points a, the angular movement of a and a' is twice the same, and is symmetrical to the y radius from the vertical line of the radius at the center of the diameter connected to a and a'. meet Although the root value of x^2=2 is two different signs, when they meet as symmetry in the end, the 'symmetry of the solution' explored by Galois in the aspect that looks like a single radius is also 'topological mathematics', a type of geometry that appeared in the 19th century. There is a conceptual similarity to the symmetry covered in '.
In that sense, the fact that one grand unified point is gathered at an arbitrary point on a vertical line and at the diagonal vertex of qpeoms in a Dedekind cut may mean that the grand unified theory of mathematics or physics ultimately gathers 'qpeoms.zz'.vixer, qvixer in one place.' . haha.
vix.a'6//vixx.a(b1,g3,k3,o5,n6)
b0acfd|0000e0
000ac0|f00bde
0c0fab|000e0d
e00d0c|0b0fa0
f000e0|b0dac0
d0f000|cae0b0
0b000f|0ead0c
0deb00|ac000f
ced0ba|00f000
a0b00e|0dc0f0
0ace00|df000b
0f00d0|e0bc0a
sample qoms (standard)
0000000011=2,0
0000001100
0000001100
0000010010
0001100000
0101000000
0010010000
0100100000
2000000000
0010000001
sample pms (standard)
q0000000000
00q00000000
0000q000000
000000q0000
00000000q00
0000000000q
0q000000000
000q0000000
00000q00000
0000000q000
000000000q0
Sample msoss
zxdxybzyz
zxdzxezxz
xxbyyxzz
zybzzfxzy
cadccbcdc
cdbdcbdbb
xzezxdyyx
zxezybzyy
bddbcbdca

댓글