.New method of wavefunction matching helps solve quantum many-body problems
http://blog.naver.com/mssoms
http://jl0620.blogspot.com
https://www.facebook.com/junggoo.lee.9
.New method of wavefunction matching helps solve quantum many-body problems
파동함수 매칭의 새로운 방법은 양자 다체 문제를 해결하는 데 도움이 됩니다

본 대학교 요하네스 자일러(Johannes Seiler) 파동함수 매칭과 Tjon 밴드. 출처: 자연 (2024). DOI: 10.1038/s41586-024-07422-z MAY 15, 2024
강력하게 상호작용하는 시스템은 양자물리학과 양자화학에서 중요한 역할을 합니다. 몬테카를로 시뮬레이션과 같은 확률론적 방법은 이러한 시스템을 조사하는 입증된 방법입니다. 그러나 이러한 방법은 소위 부호 진동이 발생할 때 한계에 도달합니다. 이 문제는 이제 독일, 터키, 미국, 중국, 한국 및 프랑스의 국제 연구진이 새로운 파동함수 매칭 방법을 사용하여 해결했습니다.
예를 들어, 질량수 50까지의 모든 핵의 질량과 반지름을 이 방법을 사용하여 계산했습니다. 결과는 측정값과 일치한다고 연구원들은 이제 Nature 저널에 보고했습니다 . 지구상의 모든 물질은 원자라고 알려진 작은 입자로 구성되어 있습니다. 각 원자에는 양성자, 중성자, 전자 등 더 작은 입자가 포함되어 있습니다. 이들 입자 각각은 양자역학의 규칙을 따릅니다. 양자 역학은 원자핵 과 같은 많은 입자로 구성된 시스템을 설명하는 양자 다체 이론의 기초를 형성합니다 .
원자핵을 연구하기 위해 핵물리학자들이 사용하는 방법 중 하나는 ab initio 접근법입니다. 기본 구성 요소와 상호 작용에 대한 설명부터 시작하여 복잡한 시스템을 설명합니다. 핵물리학의 경우 기본 구성 요소는 양성자와 중성자입니다. 순순한 계산이 대답하는 데 도움이 될 수 있는 몇 가지 주요 질문 은 원자핵의 결합 에너지와 특성, 핵 구조와 양성자와 중성자 사이의 기본 상호 작용 사이의 연결입니다.
그러나 이러한 ab initio 방법은 복잡한 상호 작용이 있는 시스템에 대해 신뢰할 수 있는 계산을 수행하는 데 어려움이 있습니다. 이러한 방법 중 하나는 양자 몬테카를로 시뮬레이션입니다. 여기서 수량은 무작위 또는 확률론적 프로세스를 사용하여 계산됩니다. 양자 몬테카를로 시뮬레이션은 효율적이고 강력할 수 있지만 부호 문제라는 중요한 약점이 있습니다. 이는 서로 상쇄되는 양수 및 음수 가중치를 갖는 프로세스에서 발생합니다. 이러한 취소로 인해 최종 예측이 부정확해집니다.
파동함수 매칭으로 알려진 새로운 접근 방식은 ab initio 방법에 대한 계산 문제를 해결하는 데 도움을 주기 위한 것입니다. Ulf-G 교수는 "이 문제는 부호 진동이 없는 간단한 모델 시스템에 대한 첫 번째 근사치의 복잡한 문제를 매핑한 다음 섭동 이론의 차이를 처리함으로써 새로운 파동함수 매칭 방법으로 해결되었습니다"라고 말했습니다. 본 대학의 헬름홀츠 방사선 및 핵물리학 연구소와 Forschungszentrum Jülich의 핵물리학 연구소 및 고급 시뮬레이션 및 분석 센터의 Meißner입니다. "예를 들어, 질량수 50까지의 모든 핵의 질량과 반지름이 계산되었으며 결과는 측정값과 일치합니다"라고 학제간 연구 분야 "모델링" 및 "물질"의 회원이기도 한 Meißner는 보고합니다.
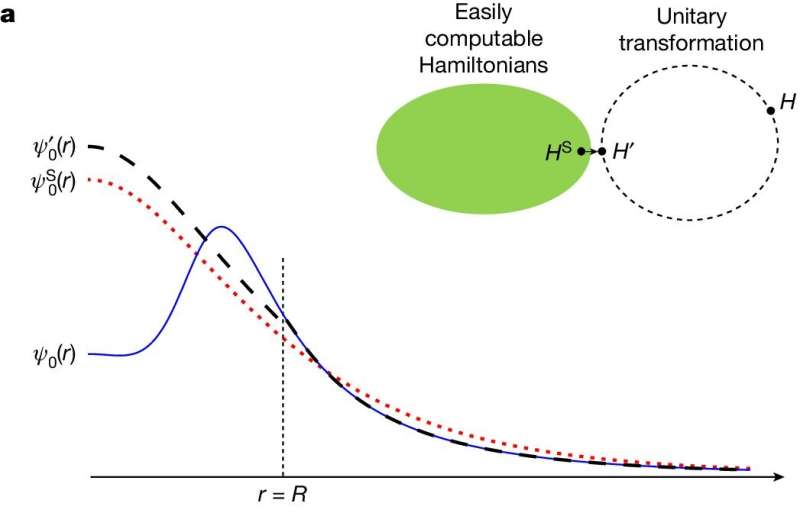
본 대학교. "양자다체이론에서는 간단한 근사 상호작용을 이용해 계산을 할 수 있지만 현실적인 고충실도 상호작용은 심각한 계산 문제를 일으키는 상황에 자주 직면합니다."라고 희귀 시설 물리학과 이학장은 말합니다. Istope Beams 및 미시간 주립대학교 물리천문학부(FRIB)이자 이론핵과학과장입니다. 파동함수 매칭은 고충실도 상호작용의 단거리 부분을 제거하고 이를 쉽게 계산 가능한 상호작용의 단거리 부분으로 대체함으로써 이 문제를 해결합니다.
-이 변환은 원래의 사실적인 상호 작용의 모든 중요한 속성을 보존하는 방식으로 수행됩니다. 새로운 파동함수는 쉽게 계산할 수 있는 상호작용과 유사하기 때문에 연구자들은 이제 쉽게 계산할 수 있는 상호작용으로 계산을 수행하고 섭동 이론이라고 불리는 작은 수정을 처리하기 위한 표준 절차를 적용할 수 있습니다.
-연구팀은 이 새로운 방법을 경핵, 중질량 핵, 중성자 물질 및 핵 물질에 대한 격자 양자 몬테카를로 시뮬레이션에 적용했습니다. 정확한 ab initio 계산을 사용하여 결과는 크기, 구조 및 결합 에너지와 같은 핵 특성에 대한 실제 데이터와 거의 일치했습니다.
부호 문제로 인해 불가능했던 계산이 이제 파동함수 매칭을 통해 수행될 수 있습니다. 연구팀은 양자 몬테카를로 시뮬레이션에만 집중했지만 파동함수 매칭은 다양한 ab initio 접근 방식에 유용할 것입니다. Meißner는 "이 방법은 예를 들어 양자 컴퓨팅에 중요한 소위 토폴로지 물질의 특성을 더 잘 예측하기 위해 고전 컴퓨팅 과 양자 컴퓨팅 모두에서 사용할 수 있습니다 ."라고 말했습니다. 첫 번째 저자는 Meißner 교수의 ERC Advanced Grant EXOTIC에서 연구원으로 2년 동안 근무한 Serdar Elhatisari 교수입니다. Meißner에 따르면 작업의 대부분이 이 기간 동안 수행되었습니다. Forschungszentrum Jülich의 슈퍼컴퓨터에서 컴퓨팅 시간의 일부는 Meißner가 이끄는 IAS-4 연구소에서 제공했습니다.
추가 정보: Serdar Elhatisari 외, 양자 다체 문제 해결을 위한 파동함수 매칭, Nature (2024). DOI: 10.1038/s41586-024-07422-z 저널 정보: 자연 본 대학교 제공
https://phys.org/news/2024-05-method-wavefunction-quantum-body-problems.html
메모 2405170315
양자입자나 심우주의 작은 빛이나 그것이 뭔 이유로 약하게 흔들린다면 섭동이다. 파동함수의 매칭은 2qms.particle(electron wave)일수도 있다.
msbase가 qpeoms에 의해 분해된다면 섭동운동은 회전축에 요란스런 흔들림을 가진다. 그러나 결국은 처음처럼 시간의 정지상태인 ms에 놓이게 된다.
여기에는 섭동이론이 존재하는 범위의 부등식이 집합 A(ems),B(msbase)구역이 존재한다. 0<A<1<B<n2, B⊂A 된다. 마치 원자핵자내에 상황을 B⊂A 로 본다. B는 무수한 질량들의 msbase 연속 분포이다. 섭동은 msbase.2d/qpeoms.3d에서 일어난다.
파동함수는 xz과 yz' 매개변수를 가진 2qms로 표현될 수 있다. 복잡한 섭동은 poms.inside에서 벌어지는 일이지만 결과값은 1이고 반지름 1의 값을 가진 두개의 구체이다. 문제는 두 구체가 작은 움직임을 주는 함수의 매칭 때문이고 확률적으로 보이는 qms.ab initio의 분포의 영향 탓일 수도 있다. 말하자면, 멀리에서 보이는 빛이 1이기는 하지만, 다른 빛이나 중력에 영향을 받아 일정하지 않는 빛의 섭동 밝기를 나타낸다. 허허.
poms 원자핵내의 양성자간에 미묘한 섭동에는 중첩되는 것들의 qms.size와 결합의 숫자들이 다를 수 있어, 매우 입자나 솔리톤 파동의 움직임이 격렬할 수도 있다.

-The research team applied this new method to lattice quantum Monte Carlo simulations of light nuclei, heavy nuclei, neutron matter, and nuclear matter. Using accurate ab initio calculations, the results closely matched real data on nuclear properties such as size, structure, and binding energy.
Perturbation theory is originally a tool for mathematically solving how the solution changes when a slight change is made to a system for which the exact solution is well known throughout physics. Except in special cases, it usually refers to perturbation theory in quantum mechanics. Therefore, this document also describes the perturbation theory of quantum mechanics.
Reference 1.
https://www.theguardian.com/science/life-and-physics/2011/oct/11/1
https://owlcation.com/stem/Different-Models-of-the-Universe-That-Challenge-the-Big-Bang-Theory
=========================
Memo 2405170315
If a quantum particle or a small light in deep space is slightly shaken for some reason, it is a perturbation. Matching the wave function may be 2qms.particle (electron wave).
If msbase is decomposed by qpeoms, the perturbation motion has a noisy shaking in the rotation axis. However, in the end, it is placed in ms, a state of stoppage in time, just like the beginning.
Here, there are regions A(ems) and B(msbase), which are sets of inequalities in the range where perturbation theory exists. 0<A<1<B<n2, B⊂A. It is as if the situation within an atomic nucleus is viewed as B⊂A. B is the msbase continuous distribution of infinite masses. The perturbation takes place in msbase.2d/qpeoms.3d.
The wavefunction can be expressed as 2qms with parameters xz and yz'. A complex perturbation is happening in poms.inside, but the result is two spheres with a radius of 1 and a radius of 1. The problem may be due to the matching of functions that give small movements of the two spheres, and may be due to the influence of the distribution of qms.ab initio, which appears stochastic. In other words, although the light seen from a distance is 1, it shows the perturbed brightness of the light that is not constant due to the influence of other lights or gravity. haha.
Poms Subtle perturbations between protons in the nucleus can cause the qms.size and number of bonds of overlap to differ, resulting in very violent motions of particles or soliton waves.
vix.a'6//vixx.a(b1,g3,k3,o5,n6)
b0acfd|0000e0
000ac0|f00bde
0c0fab|000e0d
e00d0c|0b0fa0
f000e0|b0dac0
d0f000|cae0b0
0b000f|0ead0c
0deb00|ac000f
ced0ba|00f000
a0b00e|0dc0f0
0ace00|df000b
0f00d0|e0bc0a
sample qoms (standard)
0000000011=2,0
0000001100
0000001100
0000010010
0001100000
0101000000
0010010000
0100100000
2000000000
0010000001
sample pms (standard)
q0000000000
00q00000000
0000q000000
000000q0000
00000000q00
0000000000q
0q000000000
000q0000000
00000q00000
0000000q000
000000000q0
Sample msoss
zxdxybzyz
zxdzxezxz
xxbyyxzz
zybzzfxzy
cadccbcdc
cdbdcbdbb
xzezxdyyx
zxezybzyy
bddbcbdca
댓글