.Quantum Entanglement Transforms Next-Generation Sensors

mss(magic square system)master:jk0620
http://blog.naver.com/mssoms
http://jl0620.blogspot.com
http://jk0620.tripod.com
https://www.facebook.com/junggoo.lee.9

양자 얽힘으로 차세대 센서 변화

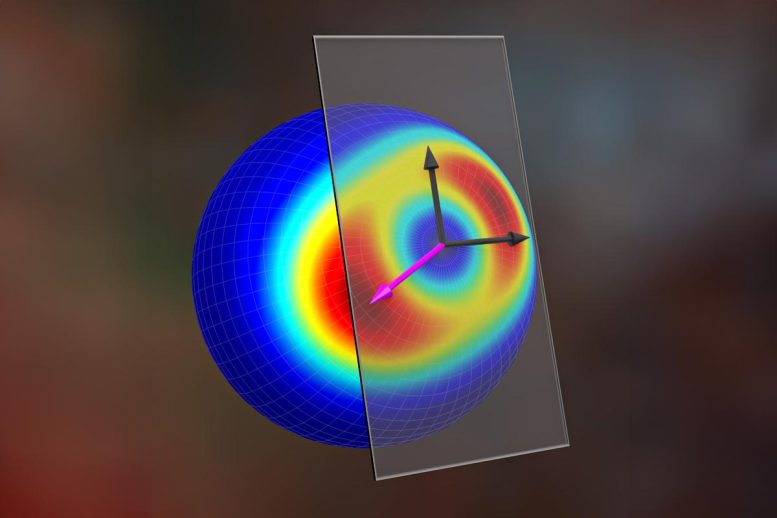
Bloch Sphere에서 최적의 생성기 찾기

주제:배우양자 물리학센서 작성자: KENNA HUGHES-CASTLEBERRY, JILA , 2024년 3월 20일 Bloch Sphere에서 최적의 생성기 찾기 Bloch 구에서 최적의 생성기를 찾는 시각화입니다. 색상은 해당 발전기의 QFI를 나타냅니다. Credit Steven Burrows/네덜란드 그룹

-연구원들은 양자 피셔 정보의 평가를 단순화하는 알고리즘을 통해 양자 감지에 혁명을 일으켰고, 이를 통해 미세한 현상을 포착하는 양자 센서의 정밀도와 유용성을 향상시켰습니다. 양자 센서는 시간 경과, 중력 변동 및 기타 효과를 가장 작은 규모로 측정하여 물리학자가 세상을 더 잘 이해하도록 돕습니다. 예를 들어, 양자 센서 중 하나인 LIGO 중력파 검출기는 레이저 빔 내의 양자 얽힘(또는 입자 간 양자 상태의 상호 의존성)을 사용하여 양성자 폭보다 최대 1000배 작은 중력파 의 거리 변화를 감지합니다! LIGO는 양자 얽힘의 힘을 활용하는 유일한 양자 센서가 아닙니다.

이는 얽힌 입자가 일반적으로 특정 매개변수에 더 민감하여 더 정확한 측정을 제공하기 때문입니다. 연구자들은 입자들 사이에 얽힘을 생성할 수 있지만, 얽힘은 때때로 관심 있는 것을 감지하는 데에만 유용할 수 있습니다.

양자 감지를 위한 양자 얽힘의 "유용성"을 측정하기 위해 물리학자들은 시스템에 대한 양자 피셔 정보(QFI)로 알려진 수학적 값을 계산합니다. 그러나 물리학자들은 시스템에 양자 상태가 많을수록 각 상태에 대해 계산할 QFI를 결정하는 것이 더 어려워진다는 사실을 발견했습니다. 이러한 문제를 극복하기 위해 JILA 펠로우 Murray Holland와 그의 연구팀은 복잡한 시스템에서 얽힌 상태의 유용성을 결정할 수 있는 수학적 값 세트인 QFIM(Quantum Fisher Information Matrix)을 사용하는 알고리즘을 제안했습니다.

편집자의 제안으로 Physical Review Letters 에 게재된 그들의 결과는 복잡한 모델 없이도 최상의 측정값을 찾는 일종의 "지름길" 역할을 함으로써 차세대 양자 센서 개발에 상당한 이점을 제공할 수 있습니다. 홀랜드는 “더 높은 수준의 시스템에서 얽힘의 유용성을 이해할 수 있는 로드맵을 마련할 수 있는 것은 양자 정보 과학의 근본적인 솔루션입니다.”라고 말했습니다.

다양한 차원을 살펴보기

양자 정보 과학(양자 감지 포함)을 연구하는 대부분의 이론 물리학자들은 Bloch 구 또는 큐비트의 가능한 모든 상태에 대한 3D 시각적 표현으로 그래픽으로 표현되는 큐비트 또는 "양자 비트"로 알려진 시스템에 중점을 둡니다. 큐비트는 SU(2) 시스템으로 간주됩니다. 여기서 SU(n)은 시스템 대칭을 활용하여 양자 세계의 사물이 어떻게 변경되고 상호 작용할 수 있는지 수학적으로 설명하는 간단한 방법입니다.

큐비트는 두 양자 수준 사이에 대칭성을 가지므로 SU(2) 시스템으로 간주되지만, 수준 수가 증가할수록 SU(n)도 마찬가지입니다. 이러한 SU(n) 시스템은 양자 얽힘을 설명할 수 있기 때문에 시스템이 다중 상태 시스템에서 얽힘과 같은 속성이 변경될 수 있는 여러 차원이나 방식을 나타낼 수 있으므로 n이 증가하면 상황이 빠르게 복잡해집니다. "SU(n) 시스템은 종이 위에 점 다발을 놓고 이 점들 사이에 빨간색, 파란색, 녹색 선을 그리는 것으로 생각할 수 있습니다."라고 논문의 공동 저자이자 공동 저자 중 한 명인 Jarrod Reilly는 설명했습니다.

홀랜드 그룹의 대학원생. 점은 다양한 양자 상태를 나타내고 선은 상태가 서로 "상호작용"하는 방식을 강조합니다. 두 개의 서로 다른 상태(자유도라고도 함)가 있는 SU(2) 시스템을 연구하는 대신 Holland와 그의 팀은 4개의 독립 상태를 설명하는 SU(4) 시스템을 살펴보았습니다. SU(4) 설정을 연구하면서 연구원들은 시스템에서 얽힘 및 기타 속성이 어떻게 변할 수 있는지에 대한 놀라운 15차원을 다루고 있다는 것을 깨달았습니다!

팀은 SU(4) 시스템의 얽힘을 최대한 활용하기 위한 간단한 무차별 대입 계산이 거의 불가능하다는 것을 빠르게 이해했습니다. “이 4단계 시스템에는 매우 복잡한 상태가 있었습니다. 우리는 그것을 시각화할 방법이 없었습니다.”라고 Holland 그룹의 대학원생이자 논문의 다른 첫 번째 공동 저자인 John Wilson이 설명했습니다. 이러한 15개 차원에 대한 QFI를 더 쉽게 계산할 수 있도록 연구원들은 QFIM을 활용하는 알고리즘을 만들어 시스템에 대해 가능한 최상의 QFI 값을 얻었습니다. “우리는 Quantum Fisher Information Matrix를 사용하여 다음과 같은 방법을 고안했습니다. 이는 주어진 복잡한 상태에 대한 수량 세트입니다. 이는 주정부가 가장 [유용한] 정보를 전달하는 수량입니다.”라고 Wilson은 덧붙였습니다.

유용성에 대한 수학적 지름길

이 알고리즘 덕분에 과학자들은 실험적으로 얽매이지 않고도 보다 복잡한 시스템에 대한 유용성 값을 제공할 수 있는 일종의 "지름길"을 갖게 되었습니다.
"복잡한 물리학을 실험하는 경우 센서의 얽힘을 어떻게 사용할 수 있는지 알아내기 위해 전체 모델이 필요하지 않습니다." 정교한 네덜란드. "좋은 센서인지 테스트하려면 감지하려는 대상의 기본 대칭만 알면 됩니다."

이 새로운 알고리즘의 또 다른 이점은 거의 모든 복잡한 양자 설정에서 작동할 수 있어 현재 수준의 양자 감지 기술을 발전시키는 물리학자들에게 유용하다는 것입니다.
Reilly는 알고리즘이 최적화 문제로 작동한다고 설명했습니다. 예를 들어 Reilly는 공을 아래로 굴리기 위해 언덕의 가장 가파른 부분(Reilly가 강조한 15차원을 가질 수 있음)을 찾으려고 가상적으로 시도하는 경우 알고리즘을 사용하여 각 방향을 확인하지 않고 이 솔루션을 계산할 수 있다고 설명했습니다.

"이 알고리즘은 연구에서 거의 상호 작용하지 않는 두 가지 최고 물리학 분야인 아인슈타인 상대성 이론의 기하학적 개념과 양자 정보(얽힘을 통해) 간의 기본 연결을 활용합니다."라고 Reilly는 덧붙였습니다. 이전 연구에서는 상태 우선 관점(센서가 먼저 생성된 다음 얽힘이 생성됨)에서 양자 얽힘의 QFI를 측정하는 방법을 검토했지만, 이 논문은 반대 접근 방식을 취한 최초의 논문 중 하나입니다.

"우리는 이러한 상태 클래스를 생성할 수 있으므로 스스로에게 질문합니다. 이를 통해 무엇을 구축할 수 있을까요?" 홀랜드가 추가되었습니다. "이것은 전체 감지 영역을 이해하는 새로운 접근 방식이자 양자 계측을 위한 강력한 방법입니다."

참조: Jarrod T. Reilly, John Drew Wilson, Simon B. Jäger, Christopher Wilson 및 Murray J. Holland의 "양자 감지를 위한 최적의 생성기", 2023년 10월 11일, Physical Review Letters .
DOI: 10.1103/PhysRevLett.131.150802

메모 240321_1436, 1530 나의 사고실험 qpeoms 스토리텔링

그동안 LIGO가 중력파를 어떻게 감지했는지 잘 알지 못했다.
자료를 보니, 양자 센서 중 하나인 LIGO 중력파 검출기는 레이저 빔 내의 양자 얽힘(또는 입자 간 양자 상태의 상호 의존성)을 사용하여 양성자 폭보다 최대 1000배 작은 중력파 의 거리 변화를 감지한다.

양자 얽힘은 msbase.oss에서 xyz으로 표현되어 2의 n 지수 값(2^n)을 가진다. xyz 문자 의 갯수가 천억개이면 2의 1000억승의 갯수가 oss.msbase이다. 허허. 그런데 중요한 사실은 2는 양자 얽힘의 값이다. abs=1을 가지는 oser 값으로 x=ef, y=ac, z=bd이다. 절대값(abs)=1은 2개의 큐비트 1+1=2,1-1=0 값을 가진 양자 단위이다. 고로 msbase.oss는 양자의 큐비트 2^n의 갯수를 가진 거대한 마방진의 은하이다. 그안에 별들이 마방진 msbase이다.

이렇듯 많은 개체는 곧바로 qpeoms에 의해 인수분해되면 양자 피셔 정보(QFI)을 가진다. 이는 다양한 매개변수를 가진 시스템의 각기 상태에서 정확한 수학적 계산을 가능하고 중력파 센서를 고감도있게 만든다.
100 billion.msbase.oss..qubit.QFI를 가지면 대략 우주 전역에 생성되는 모든 중력파를 감지할 수 있다. 어허.

No photo description available.

Source 1.
Quantum sensors can help physicists better understand the world by measuring the passage of time, gravitational fluctuations and other effects at the smallest scales. For example, one such quantum sensor, the LIGO gravitational wave detector, uses quantum entanglement (or the interdependence of quantum states between particles) within a laser beam to detect changes in the distance of gravitational waves up to 1000 times smaller than the width of a proton!
LIGO is not the only quantum sensor that harnesses the power of quantum entanglement. This is because entangled particles are generally more sensitive to certain parameters, providing more accurate measurements.
Researchers can create entanglement between particles, but entanglement can sometimes only be useful for detecting something of interest. To measure the "usefulness" of quantum entanglement for quantum sensing, physicists calculate a mathematical value known as the quantum Fisher information (QFI) for the system. But physicists have found that the more quantum states there are in a system, the more difficult it becomes to determine which QFI to calculate for each state.

====================================================
Memo 240321_1436, 1530 My thought experiment qpeoms storytelling

Until now, we did not know much about how LIGO detected gravitational waves.
The data shows that one of the quantum sensors, the LIGO gravitational wave detector, uses quantum entanglement (or the interdependence of quantum states between particles) within a laser beam to detect changes in the distance of gravitational waves that are up to 1,000 times smaller than the width of a proton.

Quantum entanglement is represented as xyz in msbase.oss, with n exponent value of 2 (2^n). If the number of xyz characters is 100 billion, the number of 2 to the power of 100 billion is oss.msbase. haha. However, the important fact is that 2 is the value of quantum entanglement. The oser value with abs=1 is x=ef, y=ac, z=bd. Absolute value (abs)=1 is a quantum unit with the values of two qubits 1+1=2,1-1=0. Therefore, msbase.oss is a huge magic square galaxy with the number of quantum qubits 2^n. The stars in it are the magic square msbase.

These many entities have quantum Fisher information (QFI) when directly factored by qpeoms. This enables accurate mathematical calculations in each state of the system with various parameters and makes the gravitational wave sensor highly sensitive.
With 100 billion.msbase.oss..qubit.QFI, we can detect approximately all gravitational waves generated throughout the universe. Uh huh.

Sample oms.vix.a (standard2)
2401030806
vix.a'6//vixx.a(b1,g3,k3,o5,n6)
b0acfd0000e0
000ac0f00bde
0c0fab000e0d
e00d0c0b0fa0
f000e0b0dac0
d0f000cae0b0
0b000f0ead0c
0deb00ac000f
ced0ba00f000
a0b00e0dc0f0
0ace00df000b
0f00d0e0bc0a

sample qoms (standard)
0000000011=2,0
0000001100
0000001100
0000010010
0001100000
0101000000
0010010000
0100100000
2000000000
0010000001

sample pms (standard)
q0000000000
00q00000000
0000q000000
000000q0000
00000000q00
0000000000q
0q000000000
000q0000000
00000q00000
0000000q000
000000000q0

Sample oss.base (standard)
zxdxybzyz
zxdzxezxz
xxbyyxzz
zybzzfxzy
cadccbcdc
cdbdcbdbb
xzezxdyyx
zxezybzyy
bddbcbdca