.Visualizing the microscopic phases of magic-angle twisted bilayer graphene
http://blog.naver.com/mssoms
http://jl0620.blogspot.com
http://jk0620.tripod.com
https://www.facebook.com/junggoo.lee.9
.Visualizing the microscopic phases of magic-angle twisted bilayer graphene
매직 앵글 트위스트 이중층 그래핀의 미세한 위상 시각화
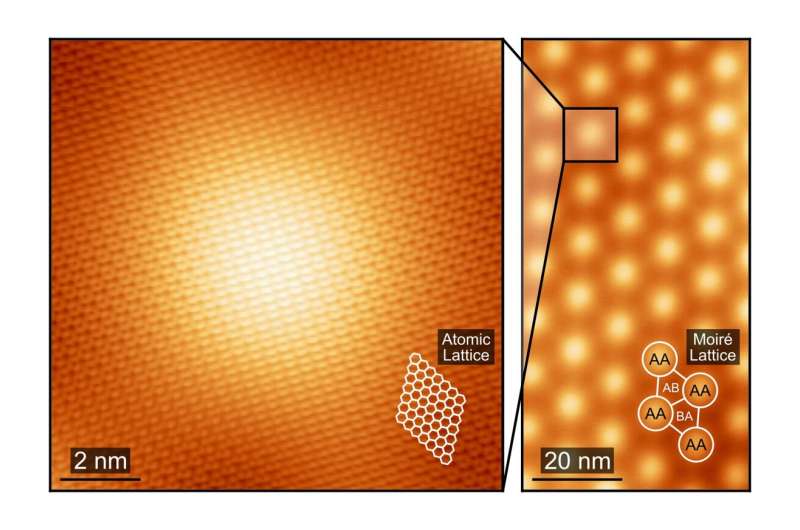
프린스턴 대학교 그래핀 원자 격자(왼쪽 패널)와 매직 앵글 그래핀 모아레 초격자(오른쪽 패널)를 보여주는 꼬인 이중층 그래핀의 주사 터널링 현미경 이미지. 제공: Kevin Nuckolls, Yazdani Group, Princeton University AUGUST 16, 2023
Princeton University가 이끄는 과학자 팀은 MATBG(magic-angle twisted bilayer graphene)로 알려진 물질에서 관찰되는 많은 양자 위상을 담당하는 정밀한 미세 토대를 이미지화했습니다. 2차원 육각형 패턴으로 배열된 탄소 원자의 뒤틀린 층으로 구성된 이 놀라운 물질은 최근 물리학, 특히 응집 물질 물리학 연구의 최전선에 있었습니다.
처음으로 연구원들은 MATBG의 절연 양자 위상을 발생시키는 상호 작용하는 전자의 미시적 거동에 대한 전례 없이 정확한 시각화를 구체적으로 포착할 수 있었습니다. 또한 참신하고 혁신적인 이론적 기술을 사용하여 이러한 행동을 해석하고 이해할 수 있었습니다. 그들의 연구는 Nature 저널에 실렸습니다 . 꼬인 이중층 그래핀 의 놀라운 특성은 MIT(Massachusetts Institute of Technology)의 Pablo Jarillo-Herrero와 그의 팀이 2018년에 처음 발견했습니다.
그들은 이 물질이 저항 없이 전자가 자유롭게 흐르는 상태인 초전도성이 될 수 있음을 보여주었습니다. 이 상태는 MRI용 자석과 입자 가속기 뿐만 아니라 양자 컴퓨터를 구축하는 데 사용되는 양자 비트(큐비트라고 함)를 만드는 등 일상적인 전자 제품의 많은 부분에 필수적입니다. 그 발견 이후, 꼬인 이중층 그래핀은 전자의 복잡한 상호 작용에 의해 생성되는 절연, 자기 및 초전도 상태와 같은 많은 새로운 양자 물리적 상태를 입증했습니다.
MATBG에서 전자가 절연 상태를 형성하는 방법과 이유는 이 분야에서 해결되지 않은 주요 퍼즐 중 하나였습니다. 이 퍼즐에 대한 해결책은 절연체와 근접 초전도체에 대한 우리의 이해를 풀어줄 뿐만 아니라 과학자들이 고온 큐레이트 초전도체를 포함하여 이해하고자 하는 많은 특이한 초전도체에 의해 공유되는 행동을 풀 것입니다. "MATBG는 단일 재료 플랫폼에서 많은 흥미로운 물리학을 보여줍니다.
그 중 많은 부분이 이해되어야 합니다."라고 이 논문의 공동 저자인 Kevin Nuckolls는 말했습니다. 2023년에 Princeton의 물리학과에 있었고 현재 MIT의 박사후 연구원입니다. "전자의 흐름이 완전히 차단되는 이 절연 단계는 정말 미스터리였습니다." 원하는 양자 효과를 생성하기 위해 연구원들은 두 장의 그래핀 시트를 서로 약간 기울인 상태에서 서로 위에 놓습니다.
-이 비스듬한 위치는 일반적인 프랑스 직물 디자인과 유사하고 그 이름을 따서 명명된 모아레 패턴을 만듭니다. 그러나 중요한 것은 그래핀의 최상층이 위치해야 하는 각도가 정확히 1.1도라는 것입니다. 이것은 양자 효과를 생성하는 "마술" 각도입니다. 즉, 이 각도는 그래핀 시트의 전자 사이에 이상하고 강한 상관 관계가 있는 상호 작용을 유도합니다.
-물리학자들은 저항이 없는 초전도 위상 및 절연 위상과 같이 이 물질에서 서로 다른 양자 위상을 입증할 수 있었지만 이러한 위상이 MATBG에서 발생하는 이유에 대한 이해는 거의 없었습니다. 실제로 MATBG와 관련된 이전의 모든 실험은 시스템이 무엇을 생성할 수 있는지에 대한 좋은 데모를 제공하지만 시스템이 이러한 상태를 생성하는 이유는 아닙니다. 그리고 그 "왜"가 현재 실험의 기초가 되었습니다.
Nuckolls는 "이 실험의 일반적인 아이디어는 전자가 그래핀 원자 규모에서 정확히 무엇을 하는지 이해하기 위해 이러한 양자 위상의 기원에 대한 질문을 던지고 싶었다"고 말했습니다. "재료를 현미경으로 조사하고 관련 상태의 이미지를 가져와 효과적으로 지문을 찍을 수 있는 능력은 우리에게 이러한 단계 중 일부의 미세한 기원을 매우 뚜렷하고 정확하게 식별할 수 있는 능력을 제공합니다. 우리의 실험은 또한 이론가들이 예측되지 않은 단계 검색." 이 연구는 2년간의 작업의 정점이며 프린스턴 대학과 버클리 캘리포니아 대학의 팀에 의해 달성되었습니다.
과학자들은 주사터널링현미경(STM)의 힘을 이용하여 이 아주 미세한 영역을 조사했습니다. 이 도구는 전자가 현미경의 날카로운 금속 팁과 샘플 사이에 깔려 있는 "양자 터널링"이라는 기술에 의존합니다. 현미경은 빛이 아닌 이 터널링 전류를 사용하여 전자의 세계를 원자 규모로 봅니다. 이러한 양자 터널링 이벤트의 측정은 고해상도의 고감도 재료 이미지로 변환됩니다. 그러나 실험 성공의 첫 번째 단계이자 아마도 가장 중요한 단계는 연구자들이 "순수한" 샘플이라고 부르는 것을 만드는 것이었습니다.
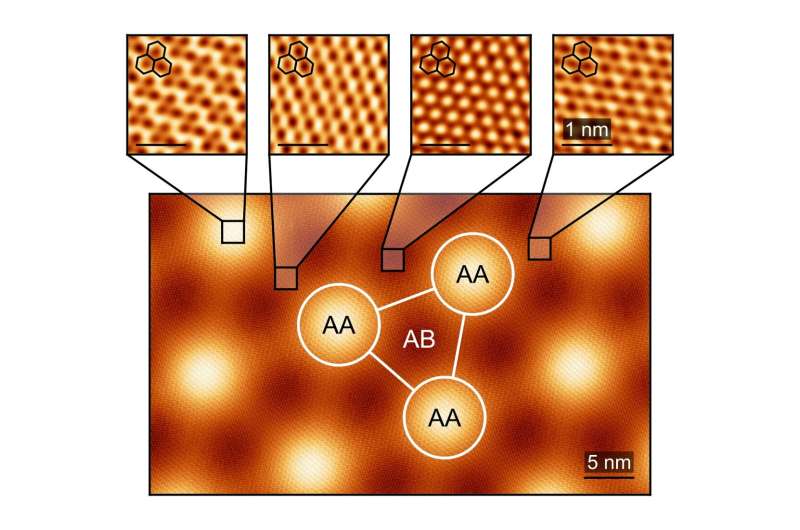
꼬인 이중층 그래핀 샘플을 구성하는 탄소 원자의 표면에는 결함이나 결함이 없어야 했습니다. 주사 터널링 현미경을 사용하여 측정한 고해상도 이미지는 매직 앵글 그래핀에서 양자 간섭 패턴을 보여줍니다. 재료 전체에서 이러한 패턴이 변경되는 방식은 연구원에게 양자 상태의 미세한 기원에 대해 알려줍니다. 제공: Kevin Nuckolls, Yazdani Group, Princeton University
-1909년 클래스 교수인 Ali Yazdani는 "이 논문을 가능하게 한 기술적 돌파구는 샘플을 청결도 면에서 매우 깨끗하게 만들어 논문에서 볼 수 있는 고해상도 이미지가 가능하도록 만드는 우리 그룹의 능력이었습니다."라고 말했습니다. Princeton University의 물리학 및 복합 재료 센터 소장. "즉, 단 하나의 결점이나 무질서 없이 10만 개의 원자를 만들어야 합니다."
-실제 실험은 그래핀 시트를 1.1도에서 정확한 "마법의 각도"로 배치하는 것과 관련이 있습니다. 그런 다음 연구원들은 그래핀 샘플 위에 STM의 날카로운 금속 팁을 놓고 샘플을 가로질러 팁을 이동하면서 양자 역학적 터널링 전류를 측정했습니다. 이 양자 규모의 전자는 입자일 뿐만 아니라 파동이기도 합니다. "그리고 본질적으로, 우리는 그들이 서로 간섭하는 정확한 방법이 기본 전자 상태를 일으키는 것에 대한 매우 구체적인 정보를 알려주는 전자의 파동과 같은 패턴을 이미징하고 있습니다."
-이 정보를 통해 연구원들은 꼬인 이중층 그래핀에 의해 생성된 양자 위상에 대해 매우 예리한 해석을 할 수 있었습니다. 중요한 것은 연구원들이 이 정보를 사용하여 이 분야에서 일하는 연구원들에게 수년 동안 도전해 온 오랜 퍼즐, 즉 그래핀이 마법의 각도에 맞춰질 때 발생하는 양자 절연 단계에 집중하고 해결했다는 것입니다.
-이론적인 관점에서 이를 이해하는 데 도움을 주기 위해 Princeton 연구원들은 Princeton의 물리학자 B. Andrei Bernevig와 Berkeley의 Michael Zaletel이 이끄는 University of California-Berkeley의 팀과 협력했습니다. 이 팀은 STM 이미지를 해석하고 전자가 절연 단계에서 수행하는 작업, 즉 전자가 상호 작용하는 방식을 이해하기 위해 "로컬 오더 매개변수" 분석이라는 새롭고 혁신적인 이론적 프레임워크를 개발했습니다.
그들이 발견한 것은 미세한 수준에서 전자 사이의 강한 반발력 때문에 절연 상태가 발생한다는 것입니다. UC Berkeley의 대학원생이자 이론가이자 이 논문의 공동 저자 중 한 명인 Tomohiro Soejima는 "매직각으로 꼬인 이중층 그래핀 에서 도전은 시스템을 모델링하는 것이었습니다."라고 말했습니다. "많은 경쟁 이론이 있었고 어느 것이 옳은지 아무도 몰랐습니다. '지문 인쇄' 실험은 절연 단계를 발생시키는 실제 전자 상호 작용을 정확히 찾아낼 수 있었기 때문에 정말 중요했습니다.
" 이 이론적인 틀을 사용함으로써 연구원들은 처음으로 관찰된 전자의 파동 함수를 측정할 수 있었습니다. "이 실험은 양자 현미경을 분석하는 새로운 방법을 소개합니다."라고 Yazdani는 말했습니다. 연구원들은 이 기술(이미지 및 이론적 프레임워크 모두)이 미래에 MATBG의 다른 많은 양자 단계를 분석하고 이해하는 데 사용될 수 있으며 궁극적으로 차세대에 유용할 수 있는 새롭고 특이한 재료 특성을 이해하는 데 도움이 될 수 있다고 제안합니다. 양자 기술 응용 프로그램. Yazdani는 "우리의 실험은 대자연이 어떻게 그렇게 복잡할 수 있는지, 정말 혼란스러울 수 있는지를 보여주는 훌륭한 예였습니다. 올바른 프레임워크를 가지고 그것을 본 다음 '오, 이런 일이 일어나고 있습니다.'라고 말할 때까지 말입니다."라고 Yazdani는 말했습니다.
추가 정보: Kevin P. Nuckolls 외, 매직 앵글 그래핀의 다체 파동 함수의 양자 텍스처, Nature (2023). DOI: 10.1038/s41586-023-06226-x 저널 정보: Nature 프린스턴대학교 제공
https://phys.org/news/2023-08-visualizing-microscopic-phases-magic-angle-bilayer.html
====================
메모 2308170558 나의 사고실험 oms 스토리텔링
모아레 패턴에서 초전도성을 나타내기 위해 6각형 시트가 필요했다. 이들 시트에는 수천억 원자가 단 하나의 결점이나 무질서 없이 시트에 배열되어야 한다. 그래야 마법의 각도 1.1에서 '신비스런 초능력이 나타난다'고 한다.
자연에는 시공간 시트에 무한대의 원자들이 왜곡된 다층 모아레 패턴층을 이룬다. 초신성 폭발로 초전도성 제트를 발산하는 것도 그 이치일거여. 허허.
그러면 수천억 구골아담이브 사이즈 갯수의 원자, 아원자를 어떻게 배열하여 로컬 오더 매개변수의 초국소성을 나타낼까? 전자들이 상호작용하는 프레임워크는 정상적으로 만들어낼 수 있나? 어려운 문제이다. 그래서 샘플링 oms.system.prame을 추천하는 바이다. 허허.

-1909 Class Professor Ali Yazdani said, "The technological breakthrough that made this paper possible was our group's ability to make the sample so clean in terms of cleanliness that the high-resolution images seen in the paper were possible." Director of the Center for Physics and Composites at Princeton University. "That means you have to make 100,000 atoms without a single flaw or disorder."
- The real experiment involved positioning the graphene sheets at the exact "magic angle" at 1.1 degrees. The researchers then placed the sharp metal tip of the STM on top of the graphene sample and measured the quantum mechanical tunneling current as they moved the tip across the sample. Electrons on this quantum scale are not only particles, but also waves. "And in essence, we're imaging wave-like patterns of electrons that tell us very specific information about exactly how they interfere with each other giving rise to the fundamental electronic state."
-This information allowed the researchers to make very incisive interpretations of the quantum phase created by twisted bilayer graphene. Importantly, the researchers used this information to focus on and solve a long-standing puzzle that has challenged researchers working in this field for years: the quantum insulation step that occurs when graphene is fitted to a magic angle.
-To help understand this from a theoretical perspective, Princeton researchers collaborated with a team at the University of California-Berkeley led by physicists B. Andrei Bernevig of Princeton and Michael Zaletel of Berkeley. The team developed a novel and innovative theoretical framework called "local order parameter" analysis to interpret STM images and understand what electrons do in the insulating phase, i.e. how they interact.
====================
memo 2308170558 my thought experiment oms storytelling
Hexagonal sheets were needed to exhibit superconductivity in moiré patterns. These sheets require hundreds of billions of atoms to be arranged in the sheet without a single defect or disorder. Only then, in the angle of magic 1.1, it is said that 'mysterious superpowers appear'.
In nature, an infinite number of atoms form a distorted multi-layered moiré pattern layer on a space-time sheet. It also makes sense that supernova explosions give off superconducting jets. haha.
Then, how to arrange atoms and subatoms of hundreds of billions of Googol Adam Eves to represent the translocality of local order parameters? Can a framework in which electrons interact normally be created? It's a hard problem. So I recommend sampling oms.system.prame. haha.
Samplea.oms (standard)
b0acfd 0000e0
000ac0 f00bde
0c0fab 000e0d
e00d0c 0b0fa0
f000e0 b0dac0
d0f000 cae0b0
0b000f 0ead0c
0deb00 ac000f
ced0ba 00f000
a0b00e 0dc0f0
0ace00 df000b
0f00d0 e0bc0a
sampleb. qoms (standard)
0000000011=2,0
0000001100
0000001100
0000010010
0001100000
0101000000
0010010000
0100100000
2000000000
0010000001
sample b.poms (standard)
q0000000000
00q00000000
0000q000000
000000q0000
00000000q00
0000000000q
0q000000000
000q0000000
00000q00000
0000000q000
000000000q0
Samplec.oss (standard)
zxdxybzyz
zxdzxezxz
xxbyyxzz
zybzzfxzy
cadccbcdc
cdbdcbdbb
xzezxdyyx
zxezybzyy
bddbcbdca

.Sharpening “Occam’s Razor” – The Mathematical Quest To Simplify Science
"Occam's Razor" 연마 - 과학을 단순화하기 위한 수학적 탐구

주제:수학인기 있는UC 얼바인UC 산타바바라 2023년 8월 13일 UNIVERSITY OF CALIFORNIA - SANTA BARBARA 작성 철학 수학
-UC Santa Barbara와 UC Irvine의 철학자들은 대칭의 역할에 초점을 맞춰 과학 이론의 기초가 되는 수학적 구조를 사용하여 과학 이론의 복잡성을 평가하는 방법을 탐구했습니다. 그들은 대칭만이 복잡성에 대한 포괄적인 비교를 제공할 수 있는지 의심하지만 이론의 고유한 구조를 이해하는 데 있어 대칭의 힘에 주목하고 다른 종류의 대칭에 대한 향후 탐구를 제안합니다. 구조와 복잡성에 대한 새로운 관점. 과학에서는 가장 간단한 설명이 종종 가장 진실을 담고 있는 "Occam's Razor"라는 개념입니다.
이 원칙은 수세기 동안 과학적 사고를 형성했지만 추상적 아이디어를 다룰 때 어떻게 평가합니까? 새 논문에서 UC Santa Barbara 와 UC Irvine 의 철학자들은 근본적인 수학을 비교하여 과학 이론의 복잡성을 측정하는 방법에 대해 논의합니다. 그들은 대칭을 사용하여 이론이 갖는 구조의 양 또는 다른 변경이 이루어질 때 동일하게 유지되는 객체의 측면을 특성화하는 것을 목표로 합니다. 많은 논의 끝에 저자는 궁극적으로 대칭이 필요한 프레임워크를 제공할지 의심합니다.
그러나 그들은 그것이 구조를 이해하는 데 왜 그렇게 훌륭한 가이드인지 밝혀냅니다. 그들의 논문은 Synthese 저널에 게재됩니다 . UC Santa Barbara의 철학과 부교수인 수석 저자인 Thomas Barrett은 "과학 이론은 종종 해석을 숨기지 않기 때문에 세상에 대해 정확히 무엇을 말하고 있는지 말하기 어려울 수 있습니다."라고 말했습니다. “특히 현대 이론. 그들은 세기가 지나면서 더 많은 수학을 얻게 될 뿐입니다.” 서로 다른 이론의 구조의 양을 이해하면 그들이 말하는 내용을 이해하는 데 도움이 될 수 있으며 서로를 선호하는 이유를 제공할 수도 있습니다.
구조는 또한 두 아이디어가 옷만 다를 뿐 실제로는 동일한 이론임을 인식하는 데 도움이 될 수 있습니다. 예를 들어, 20세기 초에 Werner Heisenberg와 Erwin Schrödinger는 양자 역학에 대한 두 가지 개별 이론을 공식화했습니다. "그리고 그들은 서로의 이론을 싫어했습니다." Barrett이 말했습니다. 슈뢰딩거는 동료의 이론이 "가시화 가능성이 부족하다"고 주장했습니다. 한편, 하이젠베르크는 슈뢰딩거의 이론이 "반발적"이라는 것을 발견하고 "슈뢰딩거가 시각화 가능성에 대해 쓴 것은 [...] 쓰레기"라고 주장했습니다. 그러나 두 개념이 근본적으로 다른 것처럼 보였지만 실제로는 동일한 예측을 했습니다. 약 10년 후, 그들의 동료인 존 폰 노이만(John von Neumann)은 공식이 수학적으로 동등하다는 것을 증명했습니다. 사과와 오렌지 수학적 물체를 검사하는 일반적인 방법은 대칭을 보는 것입니다. 아이디어는 더 많은 대칭 개체가 더 간단한 구조를 갖는다는 것입니다. 예를 들어 회전 대칭과 반사 대칭이 무한히 많은 원을 화살표가 하나만 있는 화살표와 비교해 보십시오. 이런 의미에서 원은 화살표보다 단순하며 설명하는 데 수학이 덜 필요합니다. 저자는 이 루브릭을 자동 형태를 사용하여 보다 추상적인 수학으로 확장합니다. 이러한 함수는 어떤 의미에서 서로 "동일한" 객체의 다양한 부분을 비교합니다. 자동 형태는 다양한 이론의 구조를 측정하기 위한 경험적 방법을 제공합니다. 더 복잡한 이론은 더 적은 자동 형태를 갖습니다. 2012년에 두 명의 철학자가 서로 다른 이론의 구조적 복잡성을 비교하는 방법을 제안했습니다.
수학적 객체 X는 X의 자기동형이 Y의 자기동형의 부분집합인 경우에만 적어도 다른 Y만큼의 구조를 가집니다. 원을 다시 생각해 보십시오. 이제 그것을 절반이 빨간색인 원과 비교하십시오. 이제 음영 처리된 원은 시스템에 추가된 추가 구조로 인해 이전에 사용했던 대칭 중 일부만 갖습니다. 이것은 좋은 시도였지만 동일한 유형의 대칭을 가진 개체에 너무 의존했습니다. 이것은 모양에 대해서는 잘 작동하지만 더 복잡한 수학에는 적합하지 않습니다.
싱가포르 국립 대학교의 아이작 빌헬름(Isaac Wilhelm)은 이 민감성을 수정하려고 시도했습니다. 서로의 내부 프레임워크를 보존하는 대응 관계를 찾을 수 있는 한 서로 다른 유형의 대칭 그룹을 비교할 수 있어야 합니다. 예를 들어, 청사진에 레이블을 지정하면 건물의 내부 레이아웃을 보존하는 건물과 그림 사이의 대응 관계가 설정됩니다. 그 변화는 매우 다른 수학적 이론의 구조를 비교할 수 있게 해주지만, 오답을 내뱉기도 합니다.
"안타깝게도 Wilhelm은 너무 멀리 나갔습니다." Barrett이 말했습니다. "어떤 서신으로도 충분하지 않습니다." 도전적인 노력 최근 논문에서 Barrett과 그의 공동 저자인 JB Manchak과 James Weatherall은 그들이 고려할 대칭 또는 자동 형태의 유형을 제한하여 동료의 발전을 구하려고 했습니다. 아마도 대칭 그룹이 아닌 기본 개체(예: 원과 화살표)에서 발생하는 대응만 정결합니다. 불행히도 이 시도 역시 실패했습니다.
사실 수학적 구조를 비교하기 위해 대칭을 사용하는 것은 원칙적으로 불가능할 수 있습니다. 비대칭 모양을 고려하십시오. 아마 잉크 반점일 겁니다. 글쎄요, 세상에 하나 이상의 잉크 얼룩이 있습니다. 모두 완전히 비대칭이고 서로 완전히 다릅니다. 그러나 그들은 모두 동일한 대칭 그룹(즉, 없음)을 가지므로 이러한 모든 시스템은 일부가 다른 것보다 훨씬 더 지저분하더라도 잉크 얼룩이 동일한 복잡성을 갖는 것으로 분류합니다.
이 잉크 반점 예는 우리가 물체의 대칭성을 보는 것만으로 물체의 구조적 복잡성에 대해 모든 것을 말할 수 없다는 것을 보여줍니다. Barrett이 설명했듯이 물체가 인정하는 대칭의 수는 바닥이 0입니다. 그러나 개체가 가질 수 있는 복잡성의 양에 상응하는 상한선은 없습니다. 이 불일치는 구조적 복잡성에 대한 상한선의 환상을 만듭니다. 그리고 거기에서 저자는 진정한 문제를 폭로합니다. 대칭의 개념은 구조를 설명하는 데 강력합니다.
그러나 복잡성을 철저하게 비교할 수 있을 만큼 수학적 대상과 그것이 나타내는 과학적 이론에 대한 충분한 정보를 캡처하지 못합니다. 이를 수행할 수 있는 시스템을 찾는 일은 학자들을 계속 바쁘게 만들 것입니다. 희미한 희망 대칭은 저자가 원하는 솔루션을 제공하지 못할 수도 있지만 중요한 통찰력을 발견합니다. 대칭은 물체가 자연스럽고 유기적으로 갖춰지는 개념을 다룹니다. 이러한 방식으로 서로 다른 이론과 시스템의 구조를 비교하는 데 사용할 수 있습니다. "이 아이디어는 대칭이 구조에 대한 좋은 지침인 이유에 대한 직관적인 설명을 제공합니다."라고 Barrett은 말했습니다.
저자는 철학자들이 구조를 비교하기 위해 자동동형을 사용하는 것을 포기해야 하지만 이 아이디어는 유지할 가치가 있다고 씁니다. 다행스럽게도, 자기동형은 수학에서 대칭의 유일한 종류가 아닙니다. 예를 들어, 전체 대칭만 보는 대신 로컬 영역의 대칭을 보고 이를 비교할 수도 있습니다. Barrett은 현재 이것이 어디로 이어질지 조사하고 있으며 다른 관점에서 한 구조를 정의하는 것이 무엇을 의미하는지 설명하기 위해 노력하고 있습니다. 명확성은 여전히 우리를 피하고 있지만, 이 논문은 철학자들에게 목표를 제시합니다. 우리는 이해의 정상에 이르는 이 도전적인 등반에서 우리가 얼마나 멀리 왔는지 모릅니다. 전방 경로는 안개에 가려져 있고 도달해야 할 정상조차 없을 수 있습니다. 그러나 대칭은 우리가 등반을 계속할 때 로프를 고정할 수 있는 홀드를 제공합니다.
참조: Thomas William Barrett, JB Manchak 및 James Owen Weatherall, 2023년 5월 25일, Synthese 의 "수학적 구조의 양을 비교하기 위한 자동 형태 기준" . DOI: 10.1007/s11229-023-04186-3
====================
메모 2308170625 나의 사고실험 oms 스토리텔링
우리는 우주가 3d.원형구이거나 3d타원구형으로 생각하는 경향이 있다. 하지만 그것도 평면.2차원의 원형을 회전.pi 시켰을 때 나타나는 확장성.진행성일 뿐이다. 그곳에는 시공간적으로 잠시.동시.장시적 시간성을 나타낸다. 공간적으로는 미시.정지.거시의 크기를 가진다.
이들이 샘플링 oms.vix.a(n!).wall을 통해 키랄 대칭의 회전을 보이면 우주적 대칭적 조화와 균형.질서의 철학적 개념을 가진다. 허허.

Focusing on the role of symmetry, philosophers at UC Santa Barbara and UC Irvine explored how to evaluate the complexity of scientific theories using the mathematical structures that underlie them. They doubt that symmetry alone can provide a comprehensive comparison of complexity, but note the power of symmetry in understanding the theory's unique structure and suggest future exploration of other kinds of symmetry. A new perspective on structure and complexity. In science, the simplest explanation is the concept of "Occam's Razor", which often holds the most truth.
====================
memo 2308170625 my thought experiment oms storytelling
We tend to think of the universe as either a 3d spherical sphere or a 3d elliptical sphere. However, even that is only the scalability and progression that appears when a flat, two-dimensional circle is rotated. There, it shows temporary, simultaneous, and long-term temporality in space and time. In terms of space, it has the size of micro, static, and macro.
If they show rotation of chiral symmetry through sampling oms.vix.a(n!).wall, they have a philosophical concept of cosmic symmetrical harmony, balance and order. haha.
Samplea.oms (standard)
b0acfd 0000e0
000ac0 f00bde
0c0fab 000e0d
e00d0c 0b0fa0
f000e0 b0dac0
d0f000 cae0b0
0b000f 0ead0c
0deb00 ac000f
ced0ba 00f000
a0b00e 0dc0f0
0ace00 df000b
0f00d0 e0bc0a
sampleb. qoms (standard)
0000000011=2,0
0000001100
0000001100
0000010010
0001100000
0101000000
0010010000
0100100000
2000000000
0010000001
sample b.poms (standard)
q0000000000
00q00000000
0000q000000
000000q0000
00000000q00
0000000000q
0q000000000
000q0000000
00000q00000
0000000q000
000000000q0
Samplec.oss (standard)
zxdxybzyz
zxdzxezxz
xxbyyxzz
zybzzfxzy
cadccbcdc
cdbdcbdbb
xzezxdyyx
zxezybzyy
bddbcbdca
댓글