.Physicists develop powerful alternative to dynamic density functional theory
http://blog.naver.com/mssoms
http://jl0620.blogspot.com
http://jk0620.tripod.com
https://www.facebook.com/junggoo.lee.9
.Physicists develop powerful alternative to dynamic density functional theory
물리학자들은 동적 밀도 함수 이론에 대한 강력한 대안을 개발합니다

바이로이트 대학교 Lennard-Jones 유체를 예로 사용하여 새로운 연구에서 조사한 단방향 흐름의 그림. 3차원 비평형 시스템은 x축을 따라 작용하는 역장(파란색 화살표)에 의해 동작(빨간색 화살표)으로 설정됩니다. 신용: 마티아스 슈미트 JUNE 7, 2023
-살아있는 유기체, 생태계 및 행성 지구는 물리학적 관점에서 볼 때 열 평형 상태가 아닌 매우 크고 복잡한 시스템의 예입니다. 비평형 시스템을 물리적으로 설명하기 위해 현재까지 동적 밀도 함수 이론이 사용되었습니다. 그러나 바이로이트 대학의 물리학자들이 Journal of Physics: Condensed Matter 에 게재된 기사에서 보여주듯이 이 이론에는 약점이 있습니다 .
-멱함수 이론은 인공 지능 방법과 결합하여 시간이 지남에 따라 비평형 시스템의 역학에 대한 보다 신뢰할 수 있는 설명과 예측을 가능하게 하여 훨씬 더 나은 성능을 발휘하는 것으로 입증되었습니다. 많은 입자 시스템은 원자, 전자, 분자 및 눈에 보이지 않는 기타 입자로 구성된 모든 종류의 시스템입니다. 온도가 균형을 이루고 열 흐름이 발생하지 않으면 열 평형 상태에 있습니다. 열 평형 상태 의 시스템은 외부 조건이 변경될 때만 상태가 변경됩니다. 밀도 함수 이론은 이러한 시스템 연구를 위해 맞춤 제작되었습니다. 반세기 이상 동안 화학 및 재료 과학 에서 무한한 가치를 입증했습니다 .
-이 이론의 강력한 고전적 변형을 기반으로 평형 시스템의 상태를 높은 정확도로 설명하고 예측할 수 있습니다. 동적 밀도 함수 이론(DDFT)은 이 이론의 범위를 비평형 시스템으로 확장합니다. 여기에는 상태가 외부 경계 조건에 의해 고정되지 않는 시스템의 물리적 이해가 포함됩니다. 이러한 시스템에는 고유한 추진력이 있습니다. 즉, 외부 영향을 받지 않고 상태를 변경할 수 있는 능력이 있습니다.
따라서 DDFT의 발견 및 적용 방법은 예를 들어 살아있는 유기체 또는 미세 흐름에 대한 모델 연구에 큰 관심을 끌고 있습니다. 동적 밀도 함수 이론의 오류 가능성 그러나 DDFT는 비평형 시스템을 물리적 설명에 액세스할 수 있도록 보조 구성을 사용합니다. 이러한 시스템의 지속적인 역학을 평형 상태의 시간적 순서로 변환합니다. 이로 인해 Matthias Schmidt 교수가 이끄는 바이로이트 팀이 새로운 연구에서 보여주듯이 과소평가해서는 안 되는 오류 가능성이 있습니다.
조사는 물리학에서 "Lennard-Jones 유체"로 알려진 가스의 단방향 흐름과 같은 비교적 간단한 예에 초점을 맞췄습니다. 이 비평형 시스템이 일련의 연속적인 평형 상태로 해석되면 시스템의 시간 종속 동역학에 관련된 한 가지 측면, 즉 유동장이 무시됩니다.
결과적으로 DDFT는 부정확한 설명과 예측을 제공할 수 있습니다. "우리는 동적 밀도 함수 이론이 특정 조건에서 비평형 시스템에 적용될 때 귀중한 통찰력과 제안을 제공할 수 있다는 것을 부정하지 않습니다. 그러나 문제는 유체 흐름을 예로 사용하는 연구에서 이 점에 주목하고 싶습니다. 특정 경우에 이러한 조건이 충족되는지 여부를 충분히 확실하게 결정할 수 없습니다.
DDFT는 신뢰할 수 있는 계산을 가능하게 하는 제한된 프레임워크 조건이 제공되는지 여부에 대한 제어를 제공하지 않습니다. 비평형 시스템을 이해하기 위한 대안적인 이론적 개념"이라고 이 연구의 제1 저자인 Dr. Daniel de las Heras 교수는 말합니다. 멱함수 이론이 훨씬 더 나은 성능을 보이는 것으로 입증되었습니다. 10년 동안 Matthias Schmidt 교수 주변의 연구팀은 아직 초기 단계인 물리 이론의 개발에 상당한 기여를 해왔습니다. 이 이론은 지금까지 다입자 시스템의 물리적 연구에서 매우 성공적인 것으로 입증되었습니다.
이론(PFT). 바이로이트의 물리학자들은 고전 밀도 함수 이론이 평형 시스템의 분석을 가능하게 하는 것과 동일한 정밀도와 우아함으로 비평형 시스템의 동역학을 설명할 수 있는 목표를 추구하고 있습니다. 새로운 연구에서 그들은 유체 흐름의 예를 사용하여 비평형 시스템을 이해하는 데 있어서 멱함수 이론이 DDFT보다 훨씬 우수하다는 것을 보여줍니다. PFT를 사용하면 시간의 연속적인 평형 상태 체인을 통해 우회하지 않고도 이러한 시스템의 역학을 설명할 수 있습니다. 여기서 결정적인 요인은 인공지능의 활용이다. 기계 학습은 유동장을 포함하여 시스템 고유의 역학과 관련된 모든 요소를 포함하여 유체 흐름의 시간 종속 동작을 엽니다. 이런 식으로 팀은 Lennard-Jones 유체의 흐름을 고정밀하게 제어하는 데 성공했습니다.
"우리의 조사는 멱함수 이론이 많은 입자 시스템의 동역학을 설명하고 설명하는 데 사용할 수 있는 매우 유망한 개념이라는 추가 증거를 제공합니다. 바이로이트에서 우리는 앞으로 이 이론을 비평형에 적용하여 이 이론을 더욱 정교화할 계획입니다. 우리가 연구한 유체 흐름보다 훨씬 더 복잡한 시스템 이러한 방식으로 PFT는 지금까지 우리의 연구 결과에 따라 피할 수 있는 시스템적 약점인 동적 밀도 함수 이론을 대체할 수 있습니다. 평형 시스템에 맞게 조정되고 그 가치가 입증된 PFT는 PFT의 우아한 특수 사례로 유지됩니다.
추가 정보: Daniel de las Heras 외, 관점: 동적 밀도 함수 이론을 극복하는 방법, Journal of Physics: Condensed Matter (2023). DOI: 10.1088/1361-648X/accb33
https://phys.org/news/2023-06-physicists-powerful-alternative-dynamic-density.html
===============================
메모 2306080413 나의 사고실험 OMS 스토리텔링
멱함수는 지수을 고정시키고 베이스 밑이 변하는 함수이다. 이는 샘플링 oms=1 고정 시키고
크기를 다른의 oms=1, qoms=2, ossbase.variable=n 개념이론에 속한다. 수학에서 멱함수는 거듭제곱의 지수를 고정(1,2,n)시키고 밑(base.variable)을 변수로 하는 함수이다. 우주크기를 고정시키고 자연변화를 해석하려면 멱함수 oss.base의 모델이 필요하지 않겠나? 허허.
어떤 oms가 연산법에 충실히 적용된다면 그것이 멱함수로 해석되는 동적 밀도 함수 이론(DDFT)의 비평형 확장 물리 시스템에서도 샘플링 oms.qoms.ossbase 이론이 적용된다. 허허.


.Tiny Particles, Big Surprises: The Unexpected Complexity of Catalysts
작은 입자, 큰 놀라움: 예상치 못한 촉매의 복잡성
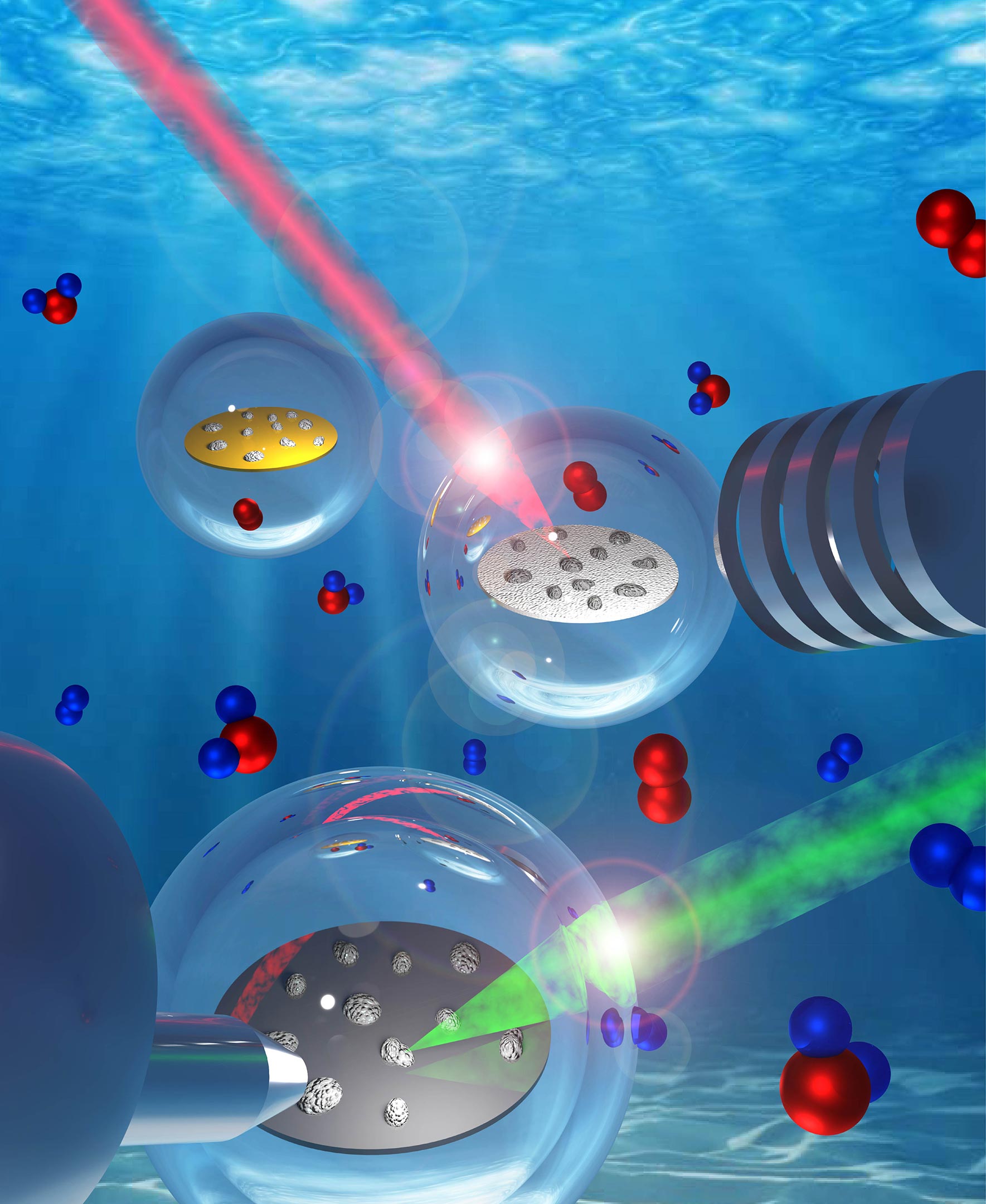
주제:촉매에너지현미경 사용비엔나 기술 대학교 By 비엔나 공과대학교 2023년 6월 7일 현미경 그림에서 촉매 작용 현미경으로 촉매. 고급 현미경 기술을 사용하는 TU Wien 연구원들은 촉매 거동의 복잡한 복잡성을 발견했습니다.
이 연구는 입자 크기, 지원 재료 특성, 온도 및 반응물 압력과 같은 요인이 촉매 활동에서 중요한 역할을 한다는 것을 발견했습니다. 개별 촉매 입자 내의 상당한 국부적 변화의 발견은 보다 복잡한 공정에 대한 향후 연구와 개선된 촉매 개발에 정보를 제공할 것입니다. 크레딧: TU 빈 JUNE 7, 2023
TU Wien에서 과학자들은 현미경 기술을 사용하여 촉매에 대한 화학 반응을 이전보다 더 정확하게 관찰하여 풍부한 세부 정보를 얻습니다. 이로 인해 일부 효과를 예측할 수 없는 이유가 명확해졌습니다. 작은 금속 입자로 구성된 촉매는 연료 전지에서 에너지 저장을 위한 합성 연료 생산에 이르기까지 많은 기술 분야에서 중요한 역할을 합니다.
그러나 촉매의 정확한 거동은 많은 세부 사항에 따라 달라지며 이들의 상호 작용은 종종 이해하기 어렵습니다. 정확히 같은 촉매를 두 번 준비하더라도 이 두 가지가 미세한 측면에서 다르고 따라서 화학적으로 매우 다르게 거동하는 경우가 종종 발생합니다. TU Wien에서 과학자들은 이러한 촉매의 다양한 위치에서 발생하는 촉매 반응을 이미지화하고 여러 가지 현미경 기술을 적용하여 이러한 효과의 원인을 식별하려고 합니다.
이러한 접근 방식은 촉매 공정에 대한 신뢰할 수 있고 미시적으로 정확한 이해를 제공합니다. 그렇게 함으로써 상대적으로 "단순한" 촉매 시스템도 예상보다 더 복잡한 것으로 나타났습니다. 예를 들어, 촉매 특성을 정의하는 것은 사용된 금속 입자의 크기 또는 지지체 재료의 화학적 성질만이 아닙니다. 단일 금속 입자 내에서도 마이크로미터 규모에서 다양한 시나리오가 우세할 수 있습니다. 수치 시뮬레이션과 함께 다양한 촉매의 거동을 설명하고 정확하게 예측할 수 있습니다.

다양한 촉매 설정 수소와 산소를 물로 전환하기 위해 9개의 서로 다른 촉매 설정이 사용되었습니다. 크레딧: TU 빈
모든 입자가 같은 것은 아니다 TU Wien 소재 화학 연구소의 Günther Rupprechter 교수는 "우리는 로듐 입자를 촉매로 사용하여 가능한 미래 에너지 운반체 수소와 산소를 연소시켜 순수한 물을 형성하는 방법을 조사했습니다."라고 설명합니다. 다양한 매개변수가 이 공정에서 중요한 역할을 합니다. 개별 로듐 입자의 크기는 얼마입니까? 어떤 서포트 재료에 결합합니까?
어떤 온도와 어떤 반응물 압력에서 반응이 일어나는가? Günther Rupprechter는 "촉매는 지지된 로듐 입자로 만들어지지만 과거에 자주 시도된 것처럼 몇 가지 간단한 매개변수로 설명할 수 있는 균일한 물체처럼 거동하지 않습니다."라고 강조합니다. “촉매 거동이 촉매 위치에 따라 크게 달라진다는 것이 곧 분명해졌습니다. 주어진 로듐 입자의 주어진 영역은 촉매적으로 활성일 수 있는 반면, 불과 마이크로미터 떨어진 다른 영역은 촉매적으로 비활성일 수 있습니다. 그리고 몇 분 후에는 상황이 역전되었을 수도 있습니다.” 한 번에 9가지 촉매 실험을 위해 저명한 저널인 ACS Catalysis에 발표된 연구의 제1 저자인 Philipp Winkler 박사는 크기가 다른 금속 입자와 다양한 지지 물질을 포함하는 9가지 촉매로 구성된 놀라운 촉매 샘플을 준비했습니다. 따라서 전용 장치에서 단일 실험으로 모든 촉매를 동시에 관찰하고 비교할 수 있습니다.
Philipp Winkler는 "현미경을 사용하여 촉매 활성 여부, 화학적 조성 및 전자 특성을 확인할 수 있습니다. 이는 샘플의 모든 개별 지점에 대해 결정됩니다."라고 말합니다. “대조적으로 기존 방법은 일반적으로 전체 샘플의 평균값을 측정합니다.
-그러나 우리가 증명한 것처럼 이것만으로는 충분하지 않은 경우가 많습니다.” 예상보다 훨씬 더 복잡하다 미시적 규모의 화학적 분석은 촉매 조성이 예상보다 훨씬 더 국부적으로 변할 수 있음을 보여주었습니다.
-개별 금속 입자 내에서도 강한 차이가 관찰되었습니다. Günther Rupprechter는 “지지 재료의 원자는 입자 위나 입자 내부로 이동하거나 표면 합금을 형성할 수도 있습니다. “어느 시점에서는 더 이상 명확한 경계가 없으며 오히려 촉매 입자와 지지체 재료 사이의 지속적인 전이가 있습니다. 화학 활동에도 영향을 미치기 때문에 이 사실을 고려하는 것이 중요합니다.” 다음 단계에서 TU Wien 팀은 얻은 통찰력과 성공적인 방법을 적용하여 훨씬 더 복잡한 촉매 공정을 해결하고, 공정을 미시적 규모로 설명하고 개선된 촉매 개발에 기여하고 새로운 촉매를 찾습니다.
참조: Philipp Winkler, Maximilian Raab, Johannes Zeininger, Lea M. Rois, Yuri Suchorski, Michael Stöger-Pollach, Matteo Amati, Rahul Parmar, Luca Gregoratti의 "촉매 반응의 현장 상관 현미경에 의한 이미징 인터페이스 및 입자 크기 효과" 및 Günther Rupprechter, 2023년 5월 23일, ACS Catalysis . DOI: 10.1021/acscatal.3c00060
https://scitechdaily.com/tiny-particles-big-surprises-the-unexpected-complexity-of-catalysts/
===============================
메모 2306080413504 나의 사고실험 OMS 스토리텔링
개별 금속 입자 내에서도 강한 차이가 관찰되었다. 지지 재료의 원자는 입자 위나 입자 내부로 이동하거나 표면 합금을 형성할 수도 있다. 어느 시점에서는 더 이상 명확한 경계가 없으며 오히려 촉매 입자와 지지체 재료 사이의 지속적인 전이가 있다.
이처럼 수많은 입자들이 복잡한 촉매공정을 겪는다면 처음부터 샘플링 oms.qoms 바탕의 입자간 촉매작용을 설계했어야 한다. 허허.
Samplea.oms (standard)
b0acfd 0000e0
000ac0 f00bde
0c0fab 000e0d
e00d0c 0b0fa0
f000e0 b0dac0
d0f000 cae0b0
0b000f 0ead0c
0deb00 ac000f
ced0ba 00f000
a0b00e 0dc0f0
0ace00 df000b
0f00d0 e0bc0a
sampleb. qoms (standard)
0000000011=2,0
0000001100
0000001100
0000010010
0001100000
0101000000
0010010000
0100100000
2000000000
0010000001
sample b.poms (standard)
q0000000000
00q00000000
0000q000000
000000q0000
00000000q00
0000000000q
0q000000000
000q0000000
00000q00000
0000000q000
000000000q0
Samplec.oss (standard)
zxdxybzyz
zxdzxezxz
xxbyyxzzx
zybzzfxzy
cadccbcdc
cdbdcbdbb
xzezxdyyx
zxezybzyy
bddbcbdca
댓글