.Fractons as information storage: Not yet tangible, but close
http://blog.naver.com/mssoms
http://jl0620.blogspot.com
http://jk0620.tripod.com
https://www.facebook.com/junggoo.lee.9
.Fractons as information storage: Not yet tangible, but close
정보 저장소로서의 프랙톤: 아직 가시적이지는 않지만 근접

Antonia Rötger, Helmholtz 독일 연구 센터 협회 수치 모델링은 전형적인 핀치 포인트(왼쪽)가 있는 분수 서명을 생성하며 중성자 산란을 통해 실험적으로 관찰할 수 있어야 합니다. 양자 변동을 허용하면 T=0K에서도 이 서명(오른쪽)이 흐려집니다. 제공: HZB MAY 26, 2023
고체의 여기도 준입자로 수학적으로 나타낼 수 있습니다. 예를 들어, 온도에 따라 증가하는 격자 진동은 포논으로 잘 설명될 수 있습니다. 수학적으로도 이전에 물질에서 관찰된 적이 없는 준입자를 설명할 수 있습니다. 그러한 "이론적인" 준입자가 흥미로운 재능을 가지고 있다면 자세히 살펴볼 가치가 있습니다. 예를 들어 프랙톤을 사용하십시오. 프랙톤은 스핀 여기의 분수이며 운동 에너지를 소유할 수 없습니다. 결과적으로 그들은 완전히 고정되어 움직이지 않습니다.
-이것은 프랙톤을 완벽하게 안전한 정보 저장을 위한 새로운 후보로 만듭니다. 특히 다른 준입자에 피기백하는 것과 같은 특수한 조건에서 이동할 수 있기 때문입니다. Freie Universität Berlin과 HZB의 이론물리학자인 Johannes Reuther 교수는 "프랙톤은 양자 전기역학의 수학적 확장에서 나타났습니다. 여기서 전기장은 벡터가 아니라 텐서로 취급되며 실제 물질과 완전히 분리됩니다."
-미래에 프랙톤을 실험적으로 관찰할 수 있으려면 가능한 한 단순한 모델 시스템을 찾는 것이 필요합니다. 따라서 반강자성으로 상호 작용하는 모서리 원자가 있는 팔면체 결정 구조가 먼저 모델링되었습니다. 이것은 스핀 상관관계에서 특징적인 핀치 포인트가 있는 특별한 패턴을 드러냈으며, 이는 원칙적으로 중성자 실험을 통해 실제 재료에서도 실험적으로 감지할 수 있습니다. "그러나 이전 연구에서 스핀은 양자 변동을 고려하지 않고 고전적인 벡터처럼 취급되었습니다."라고 Reuther는 말합니다. 이것이 Reuther가 인도 첸나이에 있는 Indian Institute of Technology의 Yasir Iqbal 및 그의 박사 과정 학생인 Nils Niggemann과 함께 처음으로 이 팔면체 고체 시스템의 계산에 양자 변동을 포함시킨 이유입니다. 이것들은 원칙적으로 프랙톤을 매핑할 수 있는 매우 복잡한 수치 계산입니다.
Niggemann은 "양자 요동이 프랙톤의 가시성을 향상시키지 않고 반대로 절대 영도에서도 프랙톤을 완전히 흐리게 하기 때문에 그 결과는 우리를 놀라게 했습니다."라고 말했습니다. 다음 단계에서 세 명의 이론물리학자는 양자 요동을 위 또는 아래로 조절할 수 있는 모델을 개발하려고 합니다 . 고전 고체 물리학과 이전 시뮬레이션 사이의 일종의 중간 세계로, 프랙톤을 포함하는 확장된 양자 전기역학 이론을 더 자세히 연구할 수 있습니다. 프랙톤을 나타내는 물질은 아직 알려져 있지 않습니다. 그러나 다음 모델이 결정 구조 와 자기적 상호 작용이 어떤 것인지에 대한 보다 정확한 표시를 제공한다면 실험 물리학자들은 그러한 물질을 설계하고 측정할 수 있을 것입니다. Reuther는 "앞으로 몇 년 안에 이러한 발견이 적용되지 않을 것으로 보이지만 아마도 앞으로 수십 년 안에 정말 새로운 속성을 가진 유명한 양자 도약이 될 것"이라고 말했습니다.
연구 결과는 Physical Review Letters 저널에 발표되었습니다 . 추가 정보: Nils Niggemann 외, 비전통적인 핀치 포인트 특이점에 대한 양자 효과, Physical Review Letters (2023). DOI: 10.1103/PhysRevLett.130.196601 저널 정보: Physical Review Letters Helmholtz 독일 연구 센터 협회 제공
https://phys.org/news/2023-05-fractons-storage-tangible.html
============================
메모 2305280624 나의 사고실험 oms 스토리텔링
스칼라는 일반적으로 존재하는 그냥 oms 값(1개) 점이다. 벡터는 스칼라가 여러개 모인것이며 차원이 높아질 수록 아래 차원의 것을 모아 놓은 선의 배열이다.
샘플링 oms는 값으로 스칼라=1이다. 샘플링 qoms는 값은 스칼라 2이다. oms 매트릭스는 면을 이룬 선들의 배열로 스칼라 값을 가진다.
텐서는 매우 수학적인 개념으로base의 내용을 가진 데이터의 배열 입체의 모습이다. 텐서의 Rank는 몇 차원만 늘려놓은 배열이다.
프랙톤은 샘플링 qoms와 같아서 양자 전자기 역학의 수학적 확장에서 나타난다. 여기서 전기장은 벡터가 아니라 텐서로 취급되며 실제 물질과 완전히 분리된 차원의 증식이 시작된다. 허허.

-This makes fractons a new candidate for perfectly secure information storage. Especially because it can move under special conditions, such as piggybacking on other quasiparticles. Professor Johannes Reuther, theoretical physicist at Freie Universität Berlin and HZB, said: "Fractons emerge in a mathematical extension of quantum electrodynamics, where the electric field is treated as a tensor rather than a vector, completely decoupled from real matter."
Note 1.
A scalar is usually just a value (one) that exists. A vector is an array of multiple scalars, and the higher the dimension, the lower the dimension.
A Tensor is a collection of arrays.
https://rekt77.tistory.com/102
============================
memo 2305280624 my thought experiment oms storytelling
A scalar is just an oms value (one) point that normally exists. A vector is a collection of several scalars, and as the dimension increases, it is an array of lines in which the lower dimension is gathered.
Sampling oms is a value scalar=1. The sampling qoms value is a scalar 2. The oms matrix is a scalar array of facet lines.
A tensor is a very mathematical concept. It is a solid shape of an array of data with the contents of a base. The rank of a tensor is an array stretched by only a few dimensions.
Fractons, like sampling qoms, appear in mathematical extensions of quantum electromagnetic mechanics. Here, the electric field is treated as a tensor rather than a vector, and the proliferation of dimensions completely separate from the actual material begins. haha.
Samplea.oms (standard)
b0acfd 0000e0
000ac0 f00bde
0c0fab 000e0d
e00d0c 0b0fa0
f000e0 b0dac0
d0f000 cae0b0
0b000f 0ead0c
0deb00 ac000f
ced0ba 00f000
a0b00e 0dc0f0
0ace00 df000b
0f00d0 e0bc0a
sampleb. qoms (standard)
0000000011=2,0
0000001100
0000001100
0000010010
0001100000
0101000000
0010010000
0100100000
2000000000
0010000001
sample b.poms (standard)
q0000000000
00q00000000
0000q000000
000000q0000
00000000q00
0000000000q
0q000000000
000q0000000
00000q00000
0000000q000
000000000q0
Samplec.oss (standard)
zxdxybzyz
zxdzxezxz
xxbyyxzzx
zybzzfxzy
cadccbcdc
cdbdcbdbb
xzezxdyyx
zxezybzyy
bddbcbdca

.The Universe is flat. Here’s what that teaches us
우주는 평평합니다. 이것이 우리에게 가르쳐주는 것입니다

이론적으로 공간 구조는 상상할 수 있는 어떤 방식으로든 휘어질 수 있습니다. 그렇다면 우리가 측정할 때 우주는 왜 평평할까요? 직선 여행 우주의 하이퍼토러스 모델에서 직선 운동은 구부러지지 않은(평평한) 시공간에서도 원래 위치로 돌아갑니다. 3D 세계가 우리에게 어떻게 보이는지에 대한 고차원적 관점에 접근하지 않고는 공간에서 그 진정한 범위와 모양을 알거나 측정할 수 없습니다.크레딧 : ESO/J.
우주의 모양은 평평할 필요가 없습니다. 그것은 더 높은 차원의 구처럼 긍정적으로 휘었을 수도 있고 더 높은 차원의 말 안장처럼 부정적으로 휘었을 수도 있습니다. 공간이 구부러질 수 있는 이유는 그 모양이 절대적인 것이 아니라 질량과 에너지 분포, 팽창률과 같은 요인의 혼합에 의해 결정되기 때문입니다. 그럼에도 불구하고 우리가 그것을 측정할 때 우리는 우리 우주가 실제로 평평하다는 것을 발견합니다. 여기에서 우리가 배울 수 있는 것과 우주적 관점에서 그것이 왜 그렇게 중요한지 알 수 있습니다.
1800년대 이전에 왔다면 우주 자체가 형태를 가질 수 있다는 생각조차 하지 못했을 것입니다. 다른 사람들과 마찬가지로 공간이 3차원 그리드에 불과하다는 유클리드의 규칙에서 시작하여 기하학을 배웠을 것입니다. 그렇다면 뉴턴의 물리 법칙을 적용하고 두 물체 사이의 힘과 같은 것이 그것을 연결하는 유일한 직선을 따라 작용할 것이라고 가정했을 것입니다. 그러나 그 이후로 우리는 이해에 있어 먼 길을 왔으며 공간 자체가 물질과 에너지의 존재에 의해 휘어질 수 있을 뿐만 아니라 그러한 효과를 목격할 수 있습니다. 우주 전체가 평면과 구별할 수 없는 공간 곡률을 가질 필요는 없었습니다.
그러나 우리의 직감이 더 높은 차원의 구와 같은 모양을 선호할 수도 있다는 사실에도 불구하고 그것은 우리가 살고 있는 우주인 것 같습니다. 우주의 모델은 다음과 같습니다. 점에서 유래, 모든 방향으로 균등하게 바깥쪽으로 확장, 최대 크기에 도달하고 중력에 의해 다시 함께 당겨지고, 그리고 결국 빅 크런치로 다시 무너지고, 20세기 전반에 걸쳐 많은 이론 물리학자들이 선호했던 것입니다. 그러나 우리가 이론적 편견을 고수하는 대신 나가서 우주를 측정하는 이유가 있습니다. 과학은 항상 실험적이고 관찰적이며 우리는 우주가 어떻게 되어야 하는지 말할 권리가 없기 때문입니다. 그리고 "평면"은 우리가 얻는 우주일 수 있지만 일반적으로 직관할 수 있는 "3차원 그리드"는 아닙니다. 평평한 우주가 무엇인지, 그렇지 않은지에 대해 알아보겠습니다.
시공간 개념을 고려할 때 이것이 프레임에 따라 지나치게 단순화되는 경우에도 공간을 3D 그리드로 시각화하는 경우가 많습니다. 실제로 시공간은 물질과 에너지의 존재에 의해 휘어지며 거리는 고정되어 있지 않고 우주가 팽창하거나 수축함에 따라 진화할 수 있습니다. 아인슈타인 이전에는 모든 사람에게 공간과 시간이 고정되고 절대적인 것으로 생각되었습니다. 오늘날 우리는 이것이 사실일 수 없음을 압니다. Credit : Reunmedia/Storyblocks

우리 대부분이 배우는 기하학인 유클리드 기하학에는 우리가 알고 있는 모든 것을 파생시킬 수 있는 다섯 가지 가정이 있습니다. 임의의 두 점이 직선 세그먼트로 연결될 수 있습니다. 모든 선분은 직선에서 무한히 확장될 수 있습니다. 모든 직선 세그먼트를 사용하여 원을 구성할 수 있습니다. 여기서 선 세그먼트의 한쪽 끝은 중심이고 다른 쪽 끝은 방사형으로 주위를 스윕합니다. 모든 직각은 서로 같고 90°(또는 π/2 라디안)를 포함합니다. 그리고 서로 평행한 두 직선은 항상 등거리를 유지하고 절대 교차하지 않습니다. 모눈종이에 그린 모든 것은 이 규칙을 따르고 우리 우주는 우리 모두에게 친숙한 유클리드 기하학의 3차원 버전을 따른다는 생각이 들었습니다. 그러나 이것은 반드시 그런 것은 아니며 다섯 번째 가정의 잘못입니다. 그 이유를 이해하려면 지구본의 경도선을 살펴보십시오. 이 지구본 다이어그램은 경도 0도에 대한 우리의 임의 정의인 본초 자오선을 중심으로 합니다. 위도선도 표시됩니다. 평평한 표면에서 평행선은 절대 교차하지 않지만 구에서는 그렇지 않습니다. 적도에서 모든 경도선은 평행하지만 모든 세로선은 북극과 남극의 두 위치에서 교차합니다.
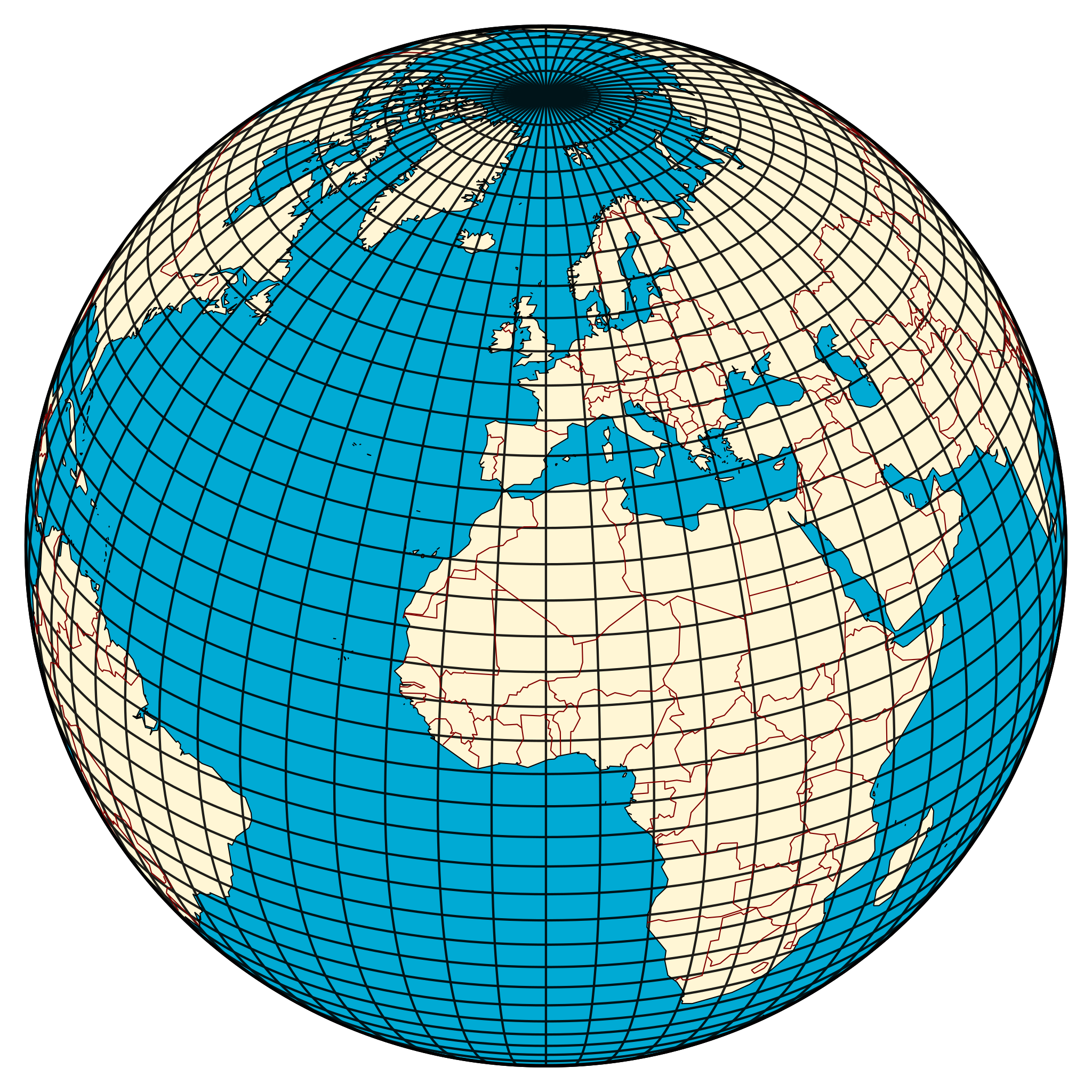
그릴 수 있는 모든 경도선은 지구 주위에 완전한 원을 그리며 적도를 가로지르고 어디에서든 90° 각도를 이룹니다. 적도는 직선이고 모든 경도선은 직선이므로 적어도 적도에서는 경도선이 평행하다는 것을 알 수 있습니다. 유클리드의 다섯 번째 가정이 참이라면 어떤 두 경도선도 절대 교차할 수 없습니다.
그러나 경도선은 교차합니다. 사실, 모든 경도선은 북극과 남극이라는 두 지점에서 교차합니다. 그 이유는 구를 "껍질을 벗기고" 정사각형을 만들기 위해 평평하게 배치할 수 없는 것과 같은 이유입니다. 구의 표면은 근본적으로 구부러져 있고 평평하지 않습니다. 사실 근본적으로 다른 세 가지 유형의 공간 표면이 있습니다. 구와 같이 양수 곡률의 표면이 있습니다. 말 안장처럼 음의 곡률을 가진 표면이 있습니다. 평평한 종이와 같이 곡률이 0인 표면이 있습니다. 곡면의 곡률을 알고 싶다면 그 위에 삼각형을 그리면 됩니다. 곡률은 삼각형이 클수록 측정하기 더 쉽습니다. 그런 다음 해당 삼각형의 세 각도를 측정하고 더합니다.
함께. 삼각형의 각도는 존재하는 공간 곡률에 따라 서로 다른 양으로 합산됩니다.
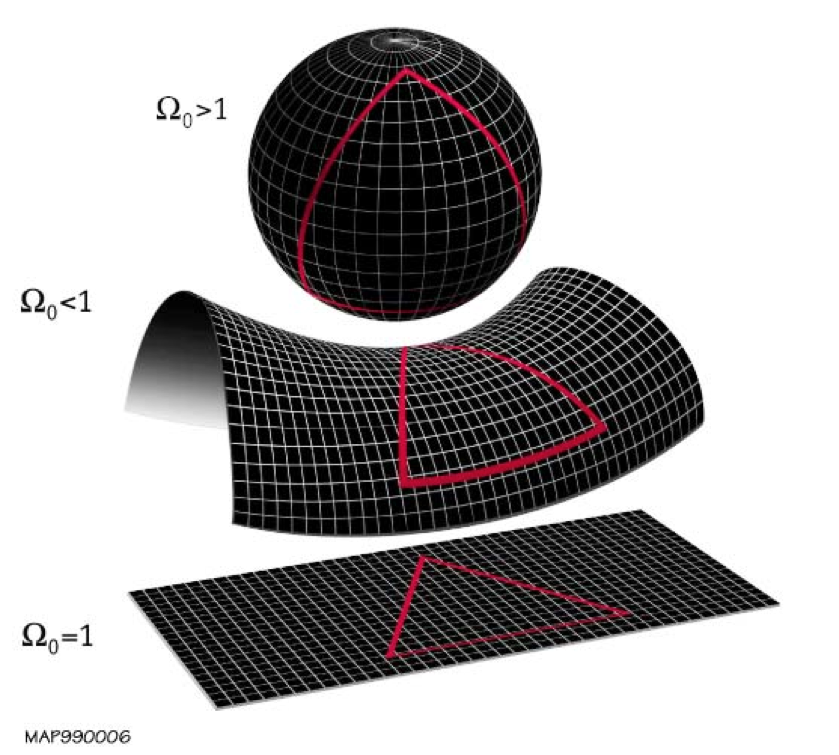
양의 곡선(상단), 음의 곡선(중간) 또는 평평한(하단) 우주는 각각 180도보다 크거나 작거나 정확히 같은 삼각형의 내부 각도를 갖습니다. ( 제공 : NASA/WMAP 과학팀) 우리 대부분은 구부러지지 않은 평평한 종이에 삼각형을 그리면 어떤 일이 일어나는지 잘 알고 있습니다. 삼각형의 세 내각의 합은 항상 180°가 됩니다. 그러나 대신 구와 같이 양의 곡률을 가진 표면이 있는 경우 각의 합은 180°보다 크며 더 큰 삼각형(구의 반지름에 비해)은 180°를 더 많이 초과합니다. 마찬가지로 안장이나 쌍곡면과 같은 음의 곡률 표면이 있는 경우 내각의 합은 항상 180° 미만이 되며 더 큰 삼각형은 표시에서 점점 더 멀어집니다. 평행선이 교차하거나 갈라질 수 있는 유클리드의 다섯 번째 가정을 따르지 않는 근본적으로 구부러진 표면을 가질 수 있다는 이러한 깨달음은 현재 거의 200년 된 비유클리드 기하학 분야로 이어졌습니다. 수학적으로 일관성 있는 비유클리드 기하학은 1823년에 Nicolai Lobachevsky와 Janos Bolyai에 의해 독립적으로 존재한다는 것이 입증되었습니다. Bernhard Riemman은 이러한 기하학을 임의의 차원으로 확장하고 오늘날 우리가 알고 있는 "메트릭 텐서"를 기록했습니다. 여기에서 다양한 매개변수는 특정 기하학이 구부러진 방식을 설명합니다. 20세기 초, 알베르트 아인슈타인은 리만의 미터법 텐서를 사용하여 시공간과 중력의 4차원 이론인 일반 상대성 이론을 개발했습니다. 중력 렌즈 현상의 삽화는 배경 은하(또는 모든 빛의 경로)가 개입하는 질량의 존재로 인해 어떻게 왜곡되는지 보여주지만, 전경 질량 자체의 존재로 인해 공간 자체가 구부러지고 왜곡되는 방식도 보여줍니다.

여러 배경 개체가 동일한 전경 렌즈로 정렬되면 적절하게 정렬된 관찰자가 여러 세트의 여러 이미지를 볼 수 있습니다. ( 제공 : NASA, ESA & L. Calçada)
간단히 말해, 아인슈타인은 어떤 상황에서도 변하지 않는 절대적인 용어로 공간과 시간을 생각하는 것이 의미가 없다는 것을 깨달았습니다. 특수 상대성 이론에서 빛의 속도에 가까운 속도로 여행하면 공간은 운동 방향을 따라 수축하고 시간은 팽창하여 서로 다른 상대 속도로 움직이는 두 관찰자에 대해 시계가 느려집니다. 관찰자에 따라 공간과 시간이 어떻게 변형되는지에 대한 규칙이 있으며, 그것은 중력이 존재하지 않는 우주에 대한 특수 상대성 이론에 불과했습니다. 그러나 우리 우주에는 중력이 있습니다. 특히 질량뿐만 아니라 모든 형태의 에너지가 존재하면 시공간 구조가 특정 방식으로 구부러지게 됩니다. 아인슈타인은 1905년(특수 상대성 이론이 출판된 때)부터 1915년(중력을 포함하는 일반 상대성 이론이 최종적이고 올바른 형태로 제시된 때)까지 꼬박 10년이 걸렸습니다. Riemann의 초기 작업에 대해. 그 결과 우리의 일반 상대성 이론은 지금까지의 모든 실험 테스트를 통과했습니다.
놀라운 점은 일반 상대성 이론의 필드 방정식을 우주에 적용할 때 물질과 에너지가 채워지고 팽창하며 등방성(모든 방향에서 동일한 평균 밀도) 및 균질(모든 위치에서 동일한 평균 밀도) ) 우주 — 우리는 다음 세 가지 사이에 복잡한 관계가 있음을 발견했습니다. 우주에 있는 모든 종류의 물질과 에너지를 합한 총량, 가장 큰 우주 규모에서 우주가 전반적으로 팽창하는 속도, 그리고 (관찰 가능한) 우주의 곡률.

뜨거운 빅뱅의 초기 순간에 우주는 극도로 뜨겁고 극도로 밀도가 높았으며 또한 극도로 빠르게 팽창했습니다. 일반 상대성 이론에서 시공간의 구조 자체가 진화하는 방식은 그 안에 있는 물질과 에너지에 완전히 의존하기 때문에 이와 같은 우주가 시간이 지남에 따라 어떻게 진화할 수 있는지에 대한 가능성은 실제로 세 가지뿐입니다. 우주 내의 물질과 에너지의 양에 비해 팽창률이 너무 낮으면 물질과 에너지의 결합된 중력 효과가 팽창률을 늦추고 정지시킨 다음 반대 방향, 수축으로 이어지는. 곧 우주는 빅 크런치로 다시 붕괴될 것입니다. 우주 내의 물질과 에너지의 양에 비해 팽창률이 너무 높으면 중력이 팽창을 멈추거나 되돌릴 수 없으며 속도를 크게 늦추지 못할 수도 있습니다. 폭주 팽창을 경험하는 우주의 위험은 매우 커서 종종 은하, 별 또는 원자의 형성을 불가능하게 만듭니다. 그러나 팽창 속도와 총 물질 및 에너지 밀도가 균형을 이룬다면 영원히 팽창하고 풍부하고 복잡한 구조를 형성하는 우주로 끝낼 수 있습니다. 이 마지막 옵션은 모든 것이 균형이 잘 잡혀 있지만 매우 초기부터 팽창 속도와 정교하게 일치하는 전체 물질 및 에너지 밀도가 필요한 우리 우주를 설명합니다. 특이 우주가 약간 더 높은 물질 밀도(빨간색)를 가졌다면 우주는 닫히고 이미 다시 붕괴되었을 것입니다. 밀도(및 음의 곡률)가 약간만 더 낮았다면 훨씬 빠르게 팽창하고 훨씬 더 커졌을 것입니다. 빅뱅은 그 자체로는 우주가 탄생하는 순간의 초기 팽창률이 전체 에너지 밀도와 완벽하게 균형을 이루어 공간적 곡률과 완벽하게 평평한 우주를 위한 공간을 전혀 남기지 않는 이유에 대해 설명하지 않습니다. 우리의 우주는 공간적으로 완벽하게 평평해 보이며 초기 총 에너지 밀도와 초기 팽창률은 최소 20개 이상의 유효 숫자로 서로 균형을 이룹니다. 크레딧 : Ned Wright의 우주론
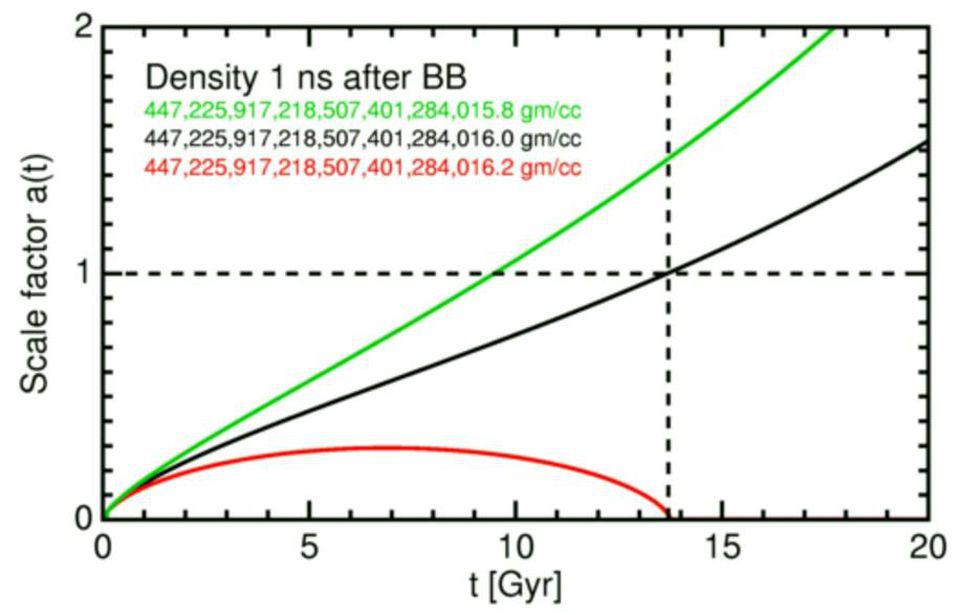
튜토리얼 우리 우주가 우리가 관찰하는 속성과 함께 존재한다는 사실은 아주 초기에 우주가 최소한 평평함에 매우 가까워야 했음을 알려줍니다. 팽창률에 비해 물질과 에너지가 너무 많은 우주는 양의 곡률을 갖는 반면 너무 적은 우주는 음의 곡률을 갖습니다. 완벽하게 균형 잡힌 케이스만 평평합니다. 그러나 우주가 매우 큰 규모로 휘어질 수 있다는 것은 가능합니다. 아마도 우리가 관찰할 수 있는 우주의 일부보다 더 클 수도 있습니다. 우리 자신의 위치와 두 개의 먼 은하 사이에 삼각형을 그려 내각을 더하는 것에 대해 생각할 수도 있지만, 우리가 할 수 있는 유일한 방법은 아직 할 수 없는 먼 은하로 여행하는 것입니다. 우리는 현재 기술적으로 우주의 작은 구석으로 제한되어 있습니다. 자신의 뒷마당에 자신을 가두어 지구의 곡률을 제대로 측정할 수 없는 것처럼 우리는 태양계에 제한을 받을 때 충분히 큰 삼각형을 만들 수 없습니다. 고맙게도 우주의 곡률을 밝히기 위해 우리가 수행할 수 있는 두 가지 주요 관측 테스트가 있으며 둘 다 동일한 결론을 지적합니다.
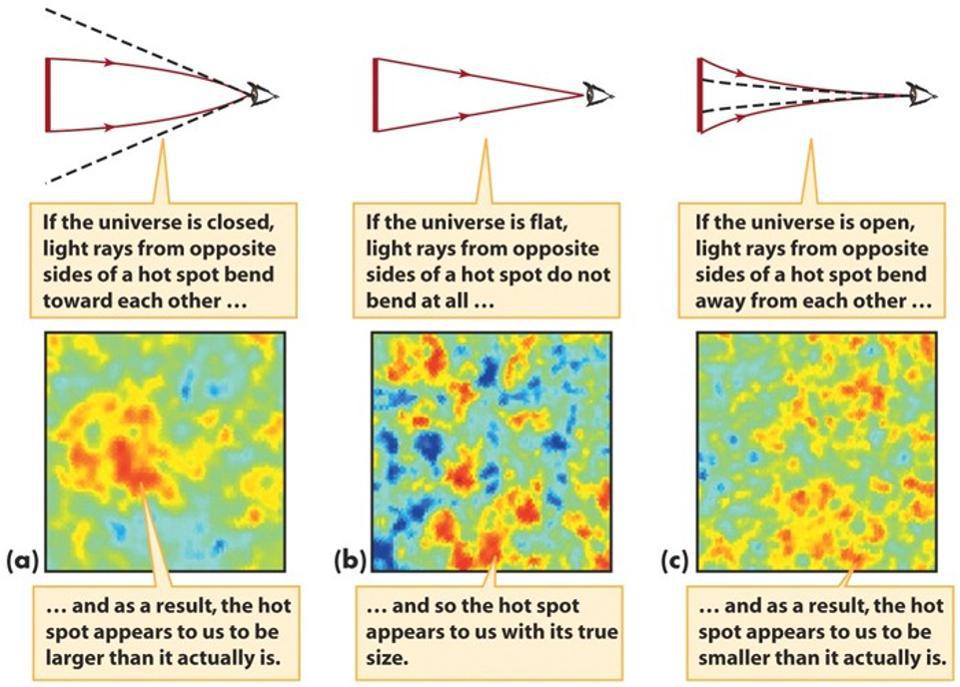
CMB에서 다양한 각도 크기의 요동이 나타나면 공간 곡률 시나리오가 달라집니다. 현재 우주는 평평한 것처럼 보이지만 우리는 약 0.4% 수준까지만 측정했습니다. 보다 정확한 수준에서 우리는 결국 어느 정도의 본질적인 곡률을 발견할 수 있지만, 우리가 관찰한 것은 우주가 구부러져 있다면 ~(250)³ 배의 규모에서만 구부러져 있다는 것을 알려주기에 충분합니다. 또는 현재 관측 가능한 우주보다 1,500만 배 이상 더 큽니다. ( 제공 : Smoot Cosmology Group/LBL) 1.)
우주 마이크로파 배경에 나타나는 온도 요동의 각 크기 . 우리 우주는 뜨거운 빅뱅의 초기 단계에서 매우 균일했지만 완벽하게 균일하지는 않았습니다. 작은 결함이 있었습니다. 평균보다 약간 더 밀집된 영역이었습니다. 물질과 에너지를 밀도가 높은 지역으로 우선적으로 끌어당기는 중력과 물질을 밀어내는 복사 사이에 발생하는 효과의 조합이 있습니다. 그 결과, 우리는 뜨거운 빅뱅에서 남겨진 관측 가능한 복사, 즉 우주 마이크로파 배경에 각인되는 일련의 온도 변동 패턴을 갖게 됩니다. 천체 물리학자 Ethan Siegel과 함께 우주를 여행하세요. 구독자는 매주 토요일 뉴스레터를 받게 됩니다. 모든 배를 타고! * 로 표시된 필드는 필수입니다. 이메일 이러한 변동에는 특정 스펙트럼이 있습니다. 특정 거리 척도에서 일정량만큼 더 뜨겁거나 더 차갑습니다. 평평한 우주에서는 그 척도가 그대로 나타나는 반면, 휘어진 우주에서는 그 척도가 더 크게(양으로 휘어진 우주에서) 또는 더 작게(음으로 휘어진 우주에서) 나타납니다. 플랑크 위성과 다른 출처에서 우리가 보는 요동의 겉보기 크기를 기반으로 우주가 평평할 뿐만 아니라 적어도 99.6% 정밀도로 평평하다는 것을 확인할 수 있습니다. 이것은 우주가 구부러져 있다면 그 구부러진 규모는 우리가 관측할 수 있는 우주의 일부보다 적어도 ~250배 더 크다는 것을 말해줍니다. 우주의 직경은 이미 ~920억 광년입니다.
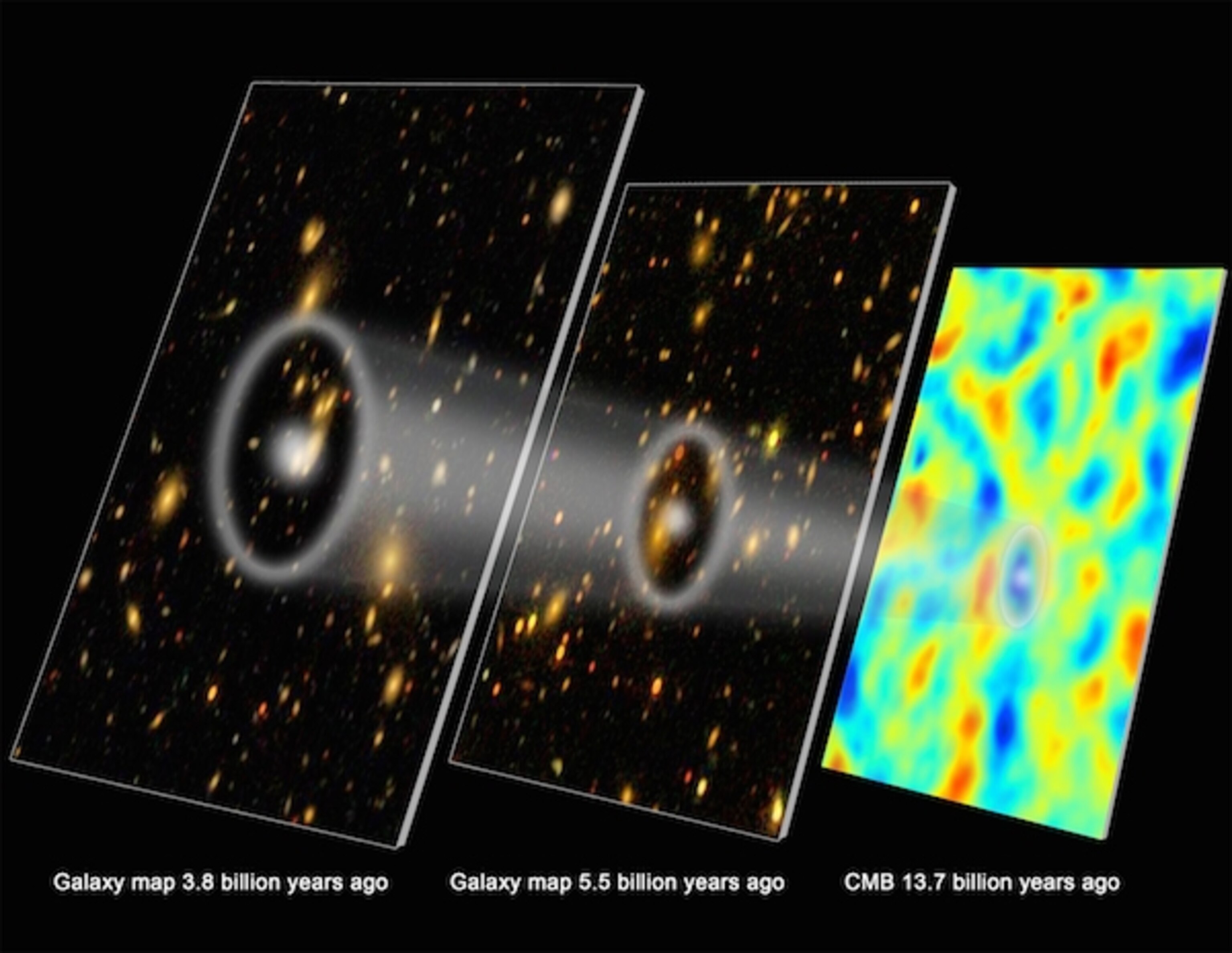
2) 우주 전체에 걸쳐 서로 다른 시대에 모여 있는 은하들 사이의 겉보기 각 분리 . 유사하게, 은하들이 모여 있을 가능성이 더 높은 특정한 거리 척도가 있습니다. 오늘날 우주의 어느 한 은하에 손가락을 대고 일정 거리를 이동했다면 "이 거리에서 다른 은하를 찾을 가능성이 얼마나 될까요?"라고 물을 수 있습니다. 매우 가까운 곳에서 은하계를 찾을 가능성이 가장 높으며 멀어짐에 따라 그 거리가 특별한 방식으로 감소한다는 것을 알게 될 것입니다. 한 가지 예외적인 개선 사항이 있습니다. -4억 또는 6억 광년보다 몇 년 더 떨어져 있습니다. 그 거리 척도는 우주가 팽창함에 따라 확장되어 초기 우주에서 "향상" 거리가 더 작아졌습니다. 그러나 우주가 양의 방향으로 또는 음의 방향으로 구부러져 있으면 이 클러스터링의 겉보기 각도 척도에 영향을 미치기 때문에 그 위에 추가 효과가 중첩될 것입니다. 특히 우주 마이크로파 배경 결과와 결합하면 null 결과가 표시된다는 사실은 훨씬 더 엄격한 제약을 제공합니다. 우주는 ~99.75% 정확도 내에서 평평합니다. 다시 말해, 우주가 휘어 있지 않다면, 예를 들어 그것이 실제로 하이퍼스피어(3차원 구의 4차원 유사체)라면, 그 하이퍼스피어는 우리가 관측할 수 있는 우주보다 최소 ~400배 더 큰 반경을 가집니다. .

-인플레이션 중에 발생하는 양자 요동은 실제로 우주 전체에 걸쳐 확장되며 나중에 더 작은 규모의 요동이 더 오래되고 더 큰 규모의 요동 위에 겹쳐집니다. 이것은 또한 이론적으로 우주 지평선보다 더 큰 규모의 요동, 즉 초지평선 요동을 생성해야 합니다. 이러한 필드 요동은 초기 우주에서 밀도 결함을 유발하고, 이는 우주 마이크로파 배경에서 측정하는 온도 요동으로 이어집니다. 출처 : E. Siegel/Beyond the Galaxy
이 모든 것은 우리가 우주가 평평하다는 것을 어떻게 아는지 말해줍니다. 그러나 그것이 평평한 이유를 이해하려면 빅뱅을 일으킨 우주적 기원 이론인 우주 인플레이션을 살펴봐야 합니다. 인플레이션은 우주를 가져갔지만 이전에는 그랬을지 모르지만 우주를 엄청난 규모로 확장했습니다. 인플레이션이 끝날 무렵에는 훨씬 더 컸습니다. 너무 커서 남은 부분이 무엇이든 우리가 관찰할 수 있는 저울의 평평한 부분과 구별할 수 없었습니다. 평탄도에 대한 유일한 예외는 인플레이션 자체 동안 우주 전체에 걸쳐 확장될 수 있는 모든 양자 요동의 합으로 인해 발생합니다. 이러한 변동이 어떻게 작용하는지에 대한 우리의 이해를 바탕으로 아직 충분히 정밀하게 테스트되지 않은 새로운 예측으로 이어집니다. 1,000,000분의 1. 우주 인플레이션 동안 우주 전체에 걸쳐 확장된 공간 고유의 양자 변동은 우주 마이크로파 배경에 각인된 밀도 변동을 발생시켰고, 이는 차례로 오늘날 우주의 별, 은하 및 기타 대규모 구조를 발생시켰습니다. 이것은 인플레이션이 선행하여 빅뱅을 설정하는 우주 전체가 어떻게 행동하는지에 대한 우리가 가진 최고의 그림입니다.

불행하게도 우리는 약 138억 년 전에 인플레이션이 끝난 한 지역의 동일한 부분의 일부인 우주 지평선 내부에 포함된 정보에만 접근할 수 있습니다. 크레딧 : E. Siegel; CMB 연구에 대한 ESA/Planck 및 DOE/NASA/NSF 기관 간 태스크 포스
현재 우리는 곡률을 400분의 1 수준까지만 측정했으며 평면과 구별할 수 없음을 발견했습니다. 그러나 우리가 이러한 극도로 민감한 정밀도에 도달할 수 있다면 우리는 이전과는 달리 우주 기원에 대한 선도적인 이론의 예측을 확인하거나 반박할 수 있는 기회를 갖게 될 것입니다. 우리는 그것의 진정한 모양이 무엇인지 알 수 없지만 그것의 곡률을 측정하고 예측할 수 있습니다. 이것은 향후 일련의 임무 및 관측 목표의 주요 목표 중 하나이며, 차세대 우주 마이크로파 배경 측정은 공간 곡률을 1/1000 이상으로 측정할 준비가 되어 있으며 로마 망원경을 사용하여 EUCLID 임무와 Rubin Observatory는 모두 온라인 상태가 되어 중입자 음향 진동 신호를 그 어느 때보다 더 정확하고 정확하게 측정할 계획이었습니다. 오늘날 우주는 평평한 것과 구별할 수 없는 것처럼 보이지만, 작지만 의미 있는 양의 0이 아닌 곡률을 가지고 있는 것으로 판명될 수 있습니다. 지금부터 한두 세대 후, 우리의 과학적 진보에 따라 결국 우리 우주가 얼마나 완벽하게 평평하지 않은지 정확히 알게 될 것입니다. 그리고 그것은 우리 우주의 기원에 대해 더 많은 것을 알려줄 수 있고 실제로 인플레이션의 어떤 풍미가 일어났는지 알려줄 수 있습니다. , 그 어떤 것보다.
https://bigthink.com/starts-with-a-bang/universe-flat/
============================
메모 2305280746 나의 사고실험 oms 스토리텔링
우주의 인플레이션은 샘플링 oss.base에서 시작된다. 베이스 우주는 빅뱅의 초기우주의 규모이다. 이곳에 전하 중력장 oss가 접목되면서 2배의 베이스가 증폭하면서 베이스와 같은 규모의 oss가 따라붙어 시공간의 질량과 에너지의 인플레이션을 급가속화 시켰다.
이들이 우주초기 어느 임계시점에서 banq.oss시작되고 banq.중력의 축압이 우주의 필라멘트 웹과 공극의 다공성을 형성한다. 이곳은 샘플링 qoms가 얽힘과 중첩의 물질의 시공간이 분리.융합되었다. 허허.

- The quantum fluctuations that occur during inflation actually extend throughout the universe, with later, smaller-scale fluctuations superimposed on older, larger-scale fluctuations. This should also theoretically create a wobble of a magnitude greater than the cosmic horizon, a hyperhorizon wobble. These field fluctuations cause density defects in the early universe, which lead to temperature fluctuations that we measure in the cosmic microwave background.
============================
memo 2305280746 my thought experiment oms storytelling
Inflation of the universe starts at sampling oss.base. The base universe is the size of the early universe of the Big Bang. As the charge gravitational field oss is grafted here, the base is amplified twice, and the oss of the same scale as the base catches up, rapidly accelerating the inflation of space-time mass and energy.
Banq.oss begins at some critical point in the early universe, and the accumulation of banq.gravity forms the porosity of the cosmic filament web and pores. This is where the sampling qoms separate and fuse the space-time of entangled and superimposed matter. haha.
Samplea.oms (standard)
b0acfd 0000e0
000ac0 f00bde
0c0fab 000e0d
e00d0c 0b0fa0
f000e0 b0dac0
d0f000 cae0b0
0b000f 0ead0c
0deb00 ac000f
ced0ba 00f000
a0b00e 0dc0f0
0ace00 df000b
0f00d0 e0bc0a
sampleb. qoms (standard)
0000000011=2,0
0000001100
0000001100
0000010010
0001100000
0101000000
0010010000
0100100000
2000000000
0010000001
sample b.poms (standard)
q0000000000
00q00000000
0000q000000
000000q0000
00000000q00
0000000000q
0q000000000
000q0000000
00000q00000
0000000q000
000000000q0
Samplec.oss (standard)
zxdxybzyz
zxdzxezxz
xxbyyxzzx
zybzzfxzy
cadccbcdc
cdbdcbdbb
xzezxdyyx
zxezybzyy
bddbcbdca
댓글