.Traditional computers can solve some quantum problems
http://blog.naver.com/mssoms
http://jl0620.blogspot.com
http://jk0620.tripod.com
https://www.facebook.com/junggoo.lee.9
.Traditional computers can solve some quantum problems
기존 컴퓨터는 일부 양자 문제를 해결할 수 있습니다
캘리포니아 공과 대학 크레딧: CC0 공개 도메인 SEPTEMBER 22, 2022
양자 컴퓨터에 대한 많은 소문이 있었고 그럴만한 이유가 있습니다. 미래형 컴퓨터는 미시적 규모에서 자연에서 일어나는 일을 모방하도록 설계되었습니다. 즉, 양자 영역을 더 잘 이해하고 의약품, 환경 친화적인 화학 물질 등을 포함한 새로운 재료의 발견을 가속화할 수 있는 능력이 있음을 의미합니다. 그러나 전문가들은 실행 가능한 양자 컴퓨터가 아직 10년 이상 남았다고 말합니다. 그 동안 연구자들은 무엇을 해야 합니까? Science 저널의 Caltech 주도의 새로운 연구는 고전 컴퓨터 에서 실행되는 기계 학습 도구를 사용하여 양자 시스템 에 대한 예측을 수행하여 연구자가 가장 까다로운 물리학 및 화학 문제를 해결하는 데 어떻게 도움이 되는지 설명합니다 . 이 개념은 이전에 실험적으로 보여졌지만 새로운 보고서는 이 방법이 작동함을 수학적으로 증명한 최초의 보고서입니다.
-"양자 컴퓨터는 많은 유형의 물리학 및 재료 과학 문제에 이상적입니다."라고 수석 저자인 Hsin-Yuan (Robert) Huang, John Preskill, Richard P. Feynman 교수, 이론 물리학 교수 및 Allen VC Davis와 함께 연구하고 있습니다. 양자 과학 기술 연구소(IQIM)의 Lenabelle Davis 리더십 의장. "하지만 우리는 아직 거기에 도달하지 않았으며 그 동안 고전적인 기계 학습 방법을 사용할 수 있다는 사실에 놀랐습니다. 궁극적으로 이 논문은 인간이 물리적 세계에 대해 배울 수 있는 것을 보여주는 것입니다."
-미시적 수준에서 물리적 세계는 양자 물리학 법칙이 지배하는 믿을 수 없을 정도로 복잡한 장소가 됩니다. 이 영역에서 입자는 상태의 중첩 또는 한 번에 두 가지 상태로 존재할 수 있습니다. 그리고 상태의 중첩은 얽힘( entanglement ), 입자가 서로 접촉하지 않고 연결되거나 상관되는 현상으로 이어질 수 있습니다. 자연 및 인공 재료에 널리 퍼져 있는 이러한 이상한 상태와 연결은 수학적으로 설명하기가 매우 어렵습니다.
"물질의 저에너지 상태를 예측하는 것은 매우 어렵습니다."라고 Huang은 말합니다. "엄청난 수의 원자가 있고 중첩되고 얽혀 있습니다. 모든 것을 설명하기 위해 방정식을 쓸 수는 없습니다." 새로운 연구는 고전적 기계 학습이 우리와 양자 세계 사이의 격차를 해소하는 데 사용될 수 있다는 최초의 수학적 시연입니다. 머신 러닝은 데이터로부터 학습하기 위해 인간의 두뇌 를 모방하는 일종의 컴퓨터 애플리케이션입니다 . Preskill은 "우리는 양자 세계에 살고 있는 고전적 존재입니다.
"우리의 두뇌와 컴퓨터는 고전적이며 이는 양자 현실과 상호 작용하고 이해하는 능력을 제한합니다." 이전 연구에서는 기계 학습 응용 프로그램이 일부 양자 문제를 해결할 수 있는 능력이 있음을 보여주었지만 이러한 방법은 일반적으로 연구자가 기계가 솔루션에 도달한 방법을 배우기 어렵게 만드는 방식으로 작동합니다. Huang은 "일반적으로 기계 학습의 경우 기계가 문제를 어떻게 해결했는지 알지 못합니다. 그것은 블랙박스입니다."라고 말합니다.
"하지만 이제 우리는 수치 시뮬레이션을 통해 기본적으로 상자에서 무슨 일이 일어나고 있는지 알아냈습니다." Huang과 그의 동료들은 Caltech의 양자 컴퓨팅을 위한 AWS 센터와 협력하여 광범위한 수치 시뮬레이션 을 수행하여 이론적 결과를 확증했습니다. 새로운 연구는 과학자들이 양자 물질의 복잡하고 특이한 단계를 더 잘 이해하고 분류하는 데 도움이 될 것입니다. "걱정은 실험실에서 새로운 양자 상태를 생성하는 사람들이 이를 이해하지 못할 수도 있다는 점이었습니다."라고 Prekill은 설명합니다.
"그러나 이제 우리는 무슨 일이 일어나고 있는지 설명하는 합리적인 고전적 데이터를 얻을 수 있습니다. 고전적 기계는 우리에게 신탁 같은 대답을 줄 뿐만 아니라 더 깊은 이해로 인도합니다." 공동 저자이자 NIST(National Institute of Standards and Technology) 물리학자인 Victor V. Albert도 동의합니다. "이 작업에서 저를 가장 흥분시키는 부분은 우리가 이제 양자 상태에 대해 사전에 많이 알 필요 없이 양자 상태의 기본 단계를 이해하는 데 도움이 되는 도구에 더 가깝다는 것입니다."
물론 궁극적으로 미래의 양자 기반 기계 학습 도구는 고전적인 방법을 능가할 것이라고 과학자들은 말합니다. 2022년 6월 10일 사이언스지에 게재 된 관련 연구 에서 Huang, Preskill 및 공동 작업자는 Google의 Sycamore 프로세서, 기초 양자 컴퓨터 를 사용하여 양자 기계 학습이 고전적 접근 방식보다 우수함을 보여주고 있습니다. "우리는 아직 이 분야의 시작 단계에 있습니다."라고 Huang은 말합니다.
"하지만 우리는 양자 머신 러닝이 결국 가장 효율적이라는 것을 알고 있습니다." 과학 연구 의 제목은 "양자 다체 문제에 대한 입증 가능한 효율적인 기계 학습"입니다. 추가 탐색 이론은 양자 컴퓨터가 고전 기계보다 일부 학습 작업에서 기하급수적으로 빨라야 한다고 제안합니다. 추가 정보: Hsin-Yuan Huang, 양자 다체 문제에 대한 Provably 효율적인 기계 학습, Science (2022). DOI: 10.1126/science.abk3333 . www.science.org/doi/10.1126/science.abk3333 저널 정보: 과학 캘리포니아 공과대학 제공
https://phys.org/news/2022-09-traditional-quantum-problems.html

-"Quantum computers are ideal for many types of physics and materials science problems," said lead author Hsin-Yuan (Robert) Huang, John Preskill, Professor Richard P. Feynman, Professor of Theoretical Physics, and Allen VC Davis. there is. Lenabelle Davis leadership chair of the Institute of Quantum Science and Technology (IQIM). "But we haven't gotten there yet, and in the meantime, I'm surprised that classical machine learning methods can be used. Ultimately, this paper is about what humans can learn about the physical world."
- At the micro level, the physical world becomes an incredibly complex place where the laws of quantum physics rule. In this realm, particles can exist in a superposition of states or in two states at once. And superposition of states can lead to entanglement, a phenomenon in which particles are connected or correlated without contacting each other. These strange states and connections pervasive in natural and man-made materials are very difficult to describe mathematically.
========================
memo 2209231715 my thought experiment oms storytelling
My quantum entanglement is shown in sample a.oms.smola_d str and the multiplicity superposition is shown in sample b.qoms. This allows for near-cosmic-scale teleportation. Real-time space internet becomes possible in the space-time of intergalactic space.
In the case of superposition, the multiplicity unit resembles a huge prime. These are placed on the linear function line in sample b.poms. This implies the existence of a multiverse as multiple superpositions of quarks occur. haha.
Sample a.oms (standard)
b0acfd 0000e0
000ac0 f00bde
0c0fab 000e0d
e00d0c 0b0fa0
f000e0 b0dac0
d0f000 cae0b0
0b000f 0ead0c
0deb00 ac000f
ced0ba 00f000
a0b00e 0dc0f0
0ace00 df000b
0f00d0 e0bc0a
sample b.qoms(standard)
0000000011=2,0
0000001100
0000001100
0000010010
0001100000
0101000000
0010010000
0100100000
2000000000
0010000001
sample b.poms(standard)
q0000000000
00q00000000
0000q000000
000000q0000
00000000q00
000000000q
0q000000000
000q0000000
00000q00000
0000000q000
000000000q0
sample c.oss(standard)
zxdxybzyz
zxdzxezxz
xxbyyxzzx
zybzzfxzy
cadccbcdc
cdbdcbdbb
xzezxdyyx
zxezybzyy
bddbcbdca

.Researchers answer fundamental question of quantum physics
연구원들은 양자 물리학의 근본적인 질문에 답합니다
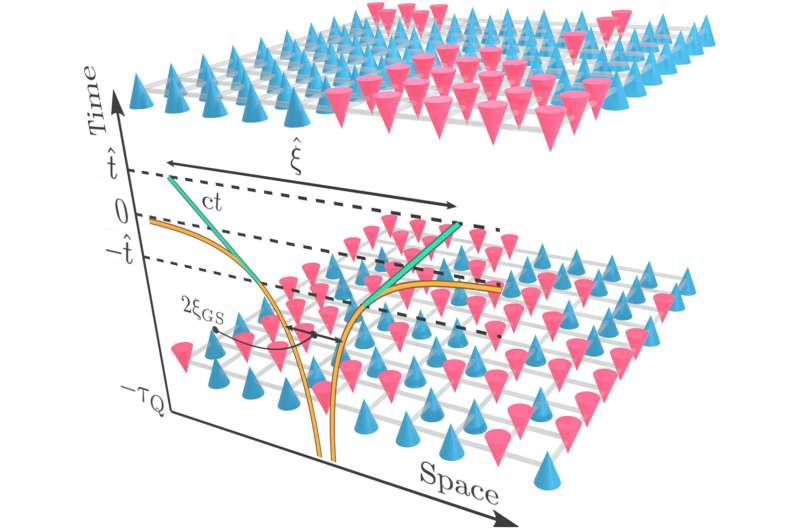
Michael Hallermayer, 아우크스부르크 대학교 2차원 스핀 1/2 모델에서 상전이에 걸친 역학의 도식적 묘사. 초기 상자성 상태(하단)에서 스핀은 횡방향 자기장의 방향과 정렬됩니다. 그런 다음 정렬 방향을 따라 해당 상태에서 스핀 구성을 측정하면 일반적으로 위쪽(파란색 원뿔) 또는 아래쪽(빨간색 원뿔)을 가리키는 무작위 패턴의 스핀이 생성됩니다. 양자 임계점을 가로질러 느린 램프 후, 시스템은 정렬 방향을 따라 스핀 구성을 측정할 때 일반적으로 그러한 도메인의 모자이크로 붕괴를 생성하는 강자성 도메인의 양자 중첩을 개발합니다(위). 전면에서 t = −τ Q 에서 시작하는 시간 t의 함수로 강자성 상관 범위의 성장을 포함합니다.램프가 임계점이 t = 0인 임계 영역을 가로질러 진행됨에 따라. Kibble-Zurek(KZ) 메커니즘에서 도메인의 크기를 결정하는 치유 길이 ξˆ는 특성 시간 ∣∣t∣에서 설정됩니다.GS는 시스템에서 해당 소리의 최대 속도 c를 초과합니다. 크레딧: 과학 발전 (2022). DOI: 10.1126/sciadv.abl6850 SEPTEMBER 22, 2022
아우크스부르크 대학(University of Augsburg)이 참여한 국제 물리학자 팀이 처음으로 양자 물리학에서 중요한 이론적 예측을 확인했습니다. 이것에 대한 계산은 너무 복잡해서 지금까지 슈퍼컴퓨터에도 너무 까다로운 것으로 판명되었습니다. 그러나 연구원들은 기계 학습 분야의 방법을 사용하여 상당히 단순화하는 데 성공했습니다. 이 연구는 양자 세계의 기본 원리에 대한 이해를 향상시킵니다. 이것은 Science Advances 저널에 게재되었습니다 .
-단일 당구공의 운동 계산은 비교적 간단합니다. 그러나 지속적으로 충돌하고 감속되고 편향되는 다수의 기체 입자의 궤적을 예측하는 것은 훨씬 더 어렵습니다. 그러나 각 입자가 얼마나 빠르게 움직이는지 전혀 명확하지 않아 주어진 시간에 확률만 다를 뿐 셀 수 없는 가능한 속도를 갖게 된다면 어떻게 될까요? 양자 세계에서도 상황은 비슷합니다.
-양자 기계적 입자는 잠재적으로 가능한 모든 속성을 동시에 가질 수도 있습니다. 이것은 양자 역학 시스템의 상태 공간을 매우 크게 만듭니다. 양자 입자가 서로 상호 작용하는 방식을 시뮬레이션하려는 경우 완전한 상태 공간을 고려해야 합니다. 아우크스부르크 대학교 물리학 연구소의 Markus Heyl 교수는 "그것은 매우 복잡합니다."라고 말합니다.
"입자의 수에 따라 계산 작업이 기하급수적으로 증가합니다. 입자가 40개가 넘으면 이미 너무 커서 가장 빠른 슈퍼컴퓨터도 처리할 수 없습니다. 이것은 양자 물리학 의 큰 도전 중 하나입니다 ." 신경망은 문제를 관리 가능하게 만듭니다. 이 문제를 단순화하기 위해 Heyl의 그룹은 기계 학습 분야의 방법인 인공 신경망 을 사용 했습니다. 이를 통해 양자 역학 상태를 재구성할 수 있습니다. "이를 통해 컴퓨터에서 관리할 수 있습니다."라고 Heyl은 설명합니다.
이 방법을 사용하여 과학자들은 지금까지 해결되지 않은 중요한 이론적 예측인 양자 Kibble-Zurek 메커니즘을 조사했습니다. 이것은 양자 상전이( quantum phase transition )라고 불리는 물리적 시스템의 동적 거동을 설명합니다 . 거시적이고 보다 직관적인 세계에서 단계 전환의 예는 물에서 얼음으로의 전환입니다. 또 다른 예는 고온에서 자석의 자기 소거입니다. 반대로 재료를 식히면 특정 임계 온도 아래에서 자석이 다시 형성되기 시작합니다. 그러나 이것은 전체 재료에 걸쳐 균일하게 발생하지 않습니다. 대신, 북극과 남극이 다르게 정렬된 많은 작은 자석이 동시에 생성됩니다. 따라서 결과 자석은 실제로 여러 다른 작은 자석의 모자이크입니다. 물리학자들은 또한 결함이 있다고 말합니다. Kibble-Zurek 메커니즘은 이러한 결함 중 예상되는 결함의 수(즉, 재료가 결국 구성되는 미니 자석의 수)를 예측합니다.
특히 흥미로운 점은 이러한 결함의 수가 보편적이어서 미세한 세부 사항과 무관하다는 것입니다. 따라서 미시적 구성이 완전히 다르더라도 많은 다른 재료가 정확하게 동일하게 거동합니다. Kibble-Zurek 메커니즘과 빅뱅 이후 은하의 형성 Kibble-Zurek 메커니즘은 원래 우주의 구조 형성을 설명하기 위해 도입되었습니다. 빅뱅 이후 우주는 처음에 완전히 균질했으며, 이는 수용된 물질이 완벽하게 고르게 분포되었음을 의미합니다. 오랫동안 은하, 태양 또는 행성이 어떻게 그런 균질한 상태에서 형성될 수 있었는지에 대해서는 불분명했습니다.
이러한 맥락에서 Kibble-Zurek 메커니즘이 설명을 제공합니다. 우주가 냉각됨에 따라 자석과 유사한 방식으로 결함이 발생했습니다. 한편 거시적 세계에서 이러한 과정은 잘 알려져 있습니다. 그러나 아직 메커니즘의 유효성을 검증할 수 없는 한 가지 유형의 상전이가 있습니다. 즉, 이전에 이미 언급한 양자 상전이입니다. "그들은 섭씨 -273도의 절대 0도 지점에서만 존재합니다."라고 Heyl은 설명합니다. "따라서 상전이는 냉각 중에 일어나지 않고 상호 작용 에너지의 변화를 통해 발생합니다. 아마도 압력 변화를 생각할 수 있습니다." 과학자들은 이제 슈퍼컴퓨터에서 그러한 양자 상전이를 시뮬레이션했습니다. 따라서 그들은 Kibble-Zurek 메커니즘이 양자 세계에서도 적용된다는 것을 처음으로 보여줄 수 있었습니다. 아우크스부르크 물리학자는 "그것은 결코 명백한 결론이 아니었습니다."라고 말합니다. "우리의 연구를 통해 많은 입자의 양자 역학 시스템 의 역학을 더 잘 설명할 수 있으므로 이 이국적인 세계를 지배하는 규칙을 더 정확하게 이해할 수 있습니다."
추가 탐색 양자 고양이를 위한 새로운 모피: 처음으로 발견된 많은 원자의 얽힘 추가 정보: Markus Schmitt et al, 2차원 횡단 필드 Ising 모델의 양자 위상 전이 역학, Science Advances (2022). DOI: 10.1126/sciadv.abl6850 저널 정보: 과학 발전 아우크스부르크 대학교 제공
https://phys.org/news/2022-09-fundamental-quantum-physics.html
======================
메모 2209231737 나의 사고실험 oms 스토리텔링
샘플a.oms.smola는 스핀 쌍방향 자유회전을 한다. 초기값 oms.a(n!) 상태에서 스핀은 횡방향 자기장의 방향과 정렬된다. 그런 다음 정렬 방향을 따라 해당 상태에서 스핀 구성을 측정하면 일반적으로 속도가 전혀 (0~+-∞)다르고 좌우 방향도 다른 smola 무작위 패턴의 스핀이 생성된다.
이들은 단지 횡방향 대칭 궤도에 존재하는 것으로 양자 기계적 smola 입자는 잠재적으로 가능한 모든 속성을 동시에 가질 수도 있는 oms=1의 값을 가진다. 허허.
샘플a.oms(standard)
b0acfd 0000e0
000ac0 f00bde
0c0fab 000e0d
e00d0c 0b0fa0
f000e0 b0dac0
d0f000 cae0b0
0b000f 0ead0c
0deb00 ac000f
ced0ba 00f000
a0b00e 0dc0f0
0ace00 df000b
0f00d0 e0bc0a
샘플b.qoms(standard)
0000000011=2,0
0000001100
0000001100
0000010010
0001100000
0101000000
0010010000
0100100000
2000000000
0010000001
샘플b.poms(standard)
q0000000000
00q00000000
0000q000000
000000q0000
00000000q00
0000000000q
0q000000000
000q0000000
00000q00000
0000000q000
000000000q0
샘플c.oss(standard)
zxdxybzyz
zxdzxezxz
xxbyyxzzx
zybzzfxzy
cadccbcdc
cdbdcbdbb
xzezxdyyx
zxezybzyy
bddbcbdca

Calculating the motion of a single billiard ball is relatively simple. However, it is much more difficult to predict the trajectory of a large number of gas particles that constantly collide, decelerate and deflect. But what if it's not at all clear how fast each particle is moving, so that at any given time it has an uncountable number of possible velocities with only different probabilities? In the quantum world, the situation is similar.
- Quantum mechanical particles can also potentially have all possible properties simultaneously. This makes the state space of quantum mechanical systems very large. If you want to simulate how quantum particles interact with each other, you must consider a complete state space. "It's very complex," says Professor Markus Heyl of the Institute of Physics at the University of Augsburg.
========================
memo 2209231737 my thought experiment oms storytelling
Sample a.oms.smola spins two-way free rotation. In the initial state oms.a(n!), the spin is aligned with the direction of the transverse magnetic field. Then, measuring the spin composition in that state along the alignment direction produces a smola random pattern of spins, usually with completely (0~+-∞) different velocities and different left and right directions.
They exist only in transversely symmetrical orbits, and quantum mechanical smola particles have a value of oms=1, which can potentially have all possible properties simultaneously. haha.
Sample a.oms (standard)
b0acfd 0000e0
000ac0 f00bde
0c0fab 000e0d
e00d0c 0b0fa0
f000e0 b0dac0
d0f000 cae0b0
0b000f 0ead0c
0deb00 ac000f
ced0ba 00f000
a0b00e 0dc0f0
0ace00 df000b
0f00d0 e0bc0a
sample b.qoms(standard)
0000000011=2,0
0000001100
0000001100
0000010010
0001100000
0101000000
0010010000
0100100000
2000000000
0010000001
sample b.poms(standard)
q0000000000
00q00000000
0000q000000
000000q0000
00000000q00
000000000q
0q000000000
000q0000000
00000q00000
0000000q000
000000000q0
sample c.oss(standard)
zxdxybzyz
zxdzxezxz
xxbyyxzzx
zybzzfxzy
cadccbcdc
cdbdcbdbb
xzezxdyyx
zxezybzyy
bddbcbdca
댓글