.NASA’s Webb Space Telescope Makes Time Critical Mid-Course Correction Burn
http://blog.naver.com/mssoms
http://jl0620.blogspot.com
http://jk0620.tripod.com
https://www.facebook.com/junggoo.lee.9

.NASA’s Webb Space Telescope Makes Time Critical Mid-Course Correction Burn
NASA의 Webb 우주 망원경은 시간이 중요한 중간 과정 수정 화상을 만듭니다

주제:제임스 웹 우주 망원경나사NASA 고다드 우주 비행 센터 NASA 작성 : 2021년 12월 25일 웹 추진기 2021년 12월 25일 오후 7시 50분(동부 표준시)에 제임스 웹 우주 망원경은 최종 궤도를 향한 궤적을 조정하기 위해 첫 번째 코스 수정 화상을 시작했습니다. 크레딧: NASA 고다드 우주 비행 센터
오후 7시 50분(동부 표준시 )에 Webb의 첫 번째 중간 코스 수정 화상이 시작되었습니다. 65분 동안 지속되었으며 이제 완료되었습니다. 이 화상은 시간이 중요한 두 가지 이정표 중 하나입니다. 첫 번째는 발사 직후 발생한 태양 전지판 배치 입니다. 이 화상은 대한 웹이의 궤도 조정 초 라그랑주 포인트 일반적으로 L2이라고도 함. 발사 후 Webb는 궤도에 진입하기 위해 자체적인 중간 추력 보정 기동을 해야 합니다. 이것은 의도적으로 설계된 것입니다.
Webb는 우주로 발사한 Ariane-5로부터 의도적으로 약간의 언더번을 받았습니다. 왜냐하면 오버스러스트를 교정할 수 없기 때문입니다. Webb가 너무 많은 추진력을 얻으면 망원경 광학 장치와 구조가 태양에 직접 노출되어 과열되고 시작하기도 전에 과학 임무가 중단되기 때문에 다시 지구를 향해 이동할 수 없습니다. 따라서 우리는 너무 많은 추력을 전달하지 않도록 주의하면서 3단계에서 올바른 속도까지 완화합니다. 총 3개의 중간 코스 수정 기동이 있습니다. 이 소각 후에는 시간이 중요한 주요 이정표가 없으므로 배포 순서, 위치, 시기 및 기간이 변경될 수 있습니다. Webb가 진행 중인 위치 를 추적 하고 향후 배포 에 대해 읽을 수 있습니다 .
NASA 는 Webb Space Telescope를 대략 2주 동안 배포할 세부 계획을 가지고 있습니다. 배포 프로세스는 자동 핸드오프 시퀀스가 아닙니다. 그것은 인간이 통제합니다. 팀은 Webb를 실시간으로 모니터링하고 언제든지 명목 배포를 일시 중지할 수 있습니다. 즉, 배포가 원래 계획된 순서나 시간에 정확히 발생하지 않을 수 있습니다.
https://scitechdaily.com/nasas-webb-space-telescope-makes-time-critical-mid-course-correction-burn/

.The earliest atmosphere on Mercury
수성의 초기 대기
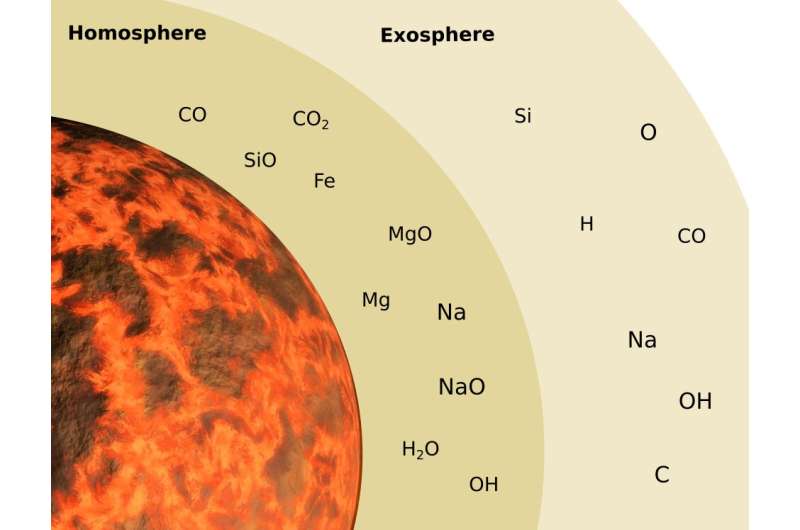
작성자: David Appell, Phys.org 수성의 초기 마그마 표면과 하층의 불균일한 대기와 상층 대기가 공간과 합쳐지는 외기권의 대기 구성 요소에 대한 개략도. 크레딧: NASA DECEMBER 23, 2021 FEATURE
-수성은 가장 특이한 행성입니다. 태양계에서 가장 작은 행성이자 태양에 가장 가까운 행성은 3:2 스핀 공명으로 천천히 회전하며 최대 섭씨 430도까지 뜨거운 열을 경험하고 밤 쪽은 섭씨 -170도까지 매우 춥습니다. . 지구에 비해 철이 풍부한 핵이 훨씬 더 크기 때문에 태양계에서 두 번째로 높은 평균 밀도를 가지며 지구보다 1.5% 낮습니다. 태양에 가까이 있음에도 불구하고 수성의 표면은 놀랍게도 나트륨과 황과 같은 휘발성 원소가 풍부한 것으로 밝혀졌습니다. 특히, 철이 풍부한 핵과 암석 맨틀(핵과 지각 사이의 지질학적 영역)으로 행성이 분리되어 있다는 사실은 수성이 형성 초기에 마그마 바다를 가지고 있었음을 시사 합니다.
다른 액체와 마찬가지로 이 바다는 증발했을 것이지만 수성의 경우 온도가 너무 높아 증기가 물이 아니라 암석으로 구성되었을 가능성이 큽니다. 행성 과학 저널(Planetary Science Journal)에 발표된 새로운 연구에서 Noah Jäggi와 동료들은 이 마그마 바다 표면의 증발이 어떻게 대기를 형성하는지 모델링하고 대기로부터의 손실이 수성의 구성을 변경할 수 있는지 여부를 결정하여 왜 적당히 휘발성 이 있는지에 대한 열린 질문을 해결했습니다.
집단수은 표면에 나트륨이 축적된 것처럼. 그들의 결과는 놀라웠다고 베른 대학의 대학원생인 Jäggi는 Phys.org에 말했습니다. 애리조나 주립 대학의 지구 및 우주 탐사 학교 책임자인 Lindy Elkins-Tanton은 초기 행성의 마그마 바다는 드문 일이 아니라고 설명했습니다. "우리는 모든 암석 행성이 형성될 때 하나 또는 그 이상(아마도 여러 개)의 마그마 바다를 가지고 있다고 생각합니다. 행성 형성의 마지막에 대한 강착의 영향은 그만큼 에너지가 넘치며 행성을 어느 정도 녹일 것입니다." 초기 태양계 는 거칠고 활동적인 장소였으며, 날아다니는 암석, 대규모 충돌 및 무거운 폭격으로 가득 차 있었습니다. 방사성 붕괴와 수성의 철이 풍부한 핵의 중력 설정에 의해 생성된 열에 더하여 이러한 사건이 생성한 열은 행성의 표면과 내부를 녹인 상태로 유지했습니다.
모델에 따르면 이러한 과정으로 인해 표면 온도가 약 2,400K(3,860°F)까지 상승했습니다. 증발과 대기 손실이 수은의 구성을 바꿀 수 있습니까? Jäggi와 그의 팀은 수성의 초기 크기 두 가지, 일부 과학자들의 가설에 따르면 오늘날보다 큰 것 하나, 그리고 가능한 마그마 해양 조성 네 가지를 가정했습니다. 이산화탄소, 일산화탄소, 수소(H2) 및 물과 같은 휘발성 종은 마그마에 용해되고 압력이 해제되면 가스로 빠져나갈 수 있습니다.
-비교적 비휘발성인 규소, 나트륨 또는 철과 같은 암석을 형성하는 원소 는 초기 마그마 바다에 존재했다고 생각 되는 매우 높은 온도 에서만 일산화규소(SiO)와 같은 기체로 존재할 수 있습니다 . 휘발성 기체 종과 비휘발성 기체 종 사이의 차이점은 주어진 온도에서 휘발성 종은 비휘발성 기체보다 평형 증기압이 훨씬 더 크다는 것입니다. 이것은 두 가지가 공존할 때 대기-마그마 표면에 대기가 가하는 압력입니다.
-연구팀은 내부-대기 결합 모델을 실행하여 해양에서 대기로 증발하는 영향을 파악하고 대기의 화학적 및 물리적 과정을 고려한 후 대기에서 우주로 또는 행성으로 되돌아 오는 질량 손실 을 확인했습니다. 한편, 행성은 냉각되고 있었습니다. 액체 마그마는 1,700K(화씨 2,600도)에서 결정화되기 시작하여 Jäggi가 사용하는 1,500K는 표면이 녹는 수명에 대한 좋은 근사값이 되며 수성의 마그마 바다에서 비롯된 질량 손실의 끝점을 설정합니다. 휘발성 및 비휘발성의 경우 마그마 바다는 증발하여 대기에 공급됩니다.
-분자는 4가지 방법 중 하나로 대기를 탈출할 수 있습니다. 하전 입자의 태양풍에서 플라즈마 가열; X-선 및 자외선 광자와 같은 극도로 고에너지 태양 광자로부터 대기 종의 광증발은 기체의 유출(유체역학적 탈출이라고도 함)을 생성하는 상부 대기 깊숙한 태양으로부터의 광자입니다. 청바지는 특히 높은 고도, 고속, 저질량 분자가 또 다른 분자 충돌을 만나기 전에 대기의 꼭대기에서 밀어내는 곳에서 탈출합니다.
고에너지 광자가 다양한 수단을 통해 탈출하는 이온을 생성하는 광이온화. 팀의 모델은 4가지 잠재적인 탈출 메커니즘 중 Jeans 탈출은 무시할 수 있는 수준이고 나머지는 수성의 형성 시기와 가열 효율에 대한 가정에 따라 초당 100만에서 40억 킬로그램의 질량 손실을 초래한다는 것을 발견했습니다. 유체역학적 탈출에서 오는 범위는 대기 종을 얼마나 효율적으로 가열하고 초기 태양에 의해 생성 및 전달되는 복사의 양에 따라 "무의미한 것에서 우세한 것까지"라고 Jäggi는 말했습니다. 그러나 중요한 것은 휘발성과 비휘발성으로 테스트된 두 개의 크게 다른 대기에서 발생한 총 질량 손실이 매우 유사한 것으로 밝혀졌다는 것입니다.
질량 손실을 감안할 때 효율적인 내부 대기 화학 교환에 대한 모델의 결과 시간 척도는 10,000년 미만이었고 대기 탈출 과정은 수성의 초기 질량의 약 0.3%, 즉 지각의 2.3km 미만을 설명합니다. (현재 수성의 반지름은 2,440km입니다.) 따라서 누적 질량 손실은 마그마 해양 단계에서 수성의 벌크 맨틀 구성을 크게 수정하지 않은 것으로 보입니다. 따라서 유도된 온실 효과에 따라 달라지는 냉각 시간은 마그마 바다의 수명 동안 손실되는 물질의 양을 결정합니다. 유체역학적 탈출을 제외하고 수성으로부터의 총 대기 질량 손실의 무의미함은 놀라웠다고 Jäggi는 말했다. "모델링된 손실률과 마그마 해양 수명 을 고려할 때 상당한 양으로 축적되거나 손실될 수 없기 때문에 수성 표면의 높은 나트륨 측정값에 더 많은 것이 있어야 함을 알려줍니다 ." 그 결과는 뜨거운 마그마 단계에서 시작하는 외계 행성 또는 지구와 같은 행성인 달로 확장될 수 있으며 "구성 요소에 의해 전달되는 변동 예산"이 있습니다.
추가 탐색 새로운 연구는 지구의 독특한 화학 성분을 설명합니다. 추가 정보: Noah Jäggi et al, Evolution of Mercury's Earliest Atmosphere, The Planetary Science Journal (2021). DOI: 10.3847/PSJ/ac2dfb 저널 정보: 행성 과학 저널
https://phys.org/news/2021-12-earliest-atmosphere-mercury.html
==================
메모 2112261522 나의 사고실험 oms스토리텔링
원소에 대해 oms이론은 vix원자핵에 대해 viger 쿼크장 oms으로 그 원소의 휘발성과 비휘발성 혹은 가볍고 무거운 것을 분류하는데 사용할 것이다.
가벼운 원소는 양성자와 중성자가 적다. 그러면 무거운 원소는 상대적으로 그 양성자와 중성자가 많다는 뜻이다. 여기서 양성자는 1q=22-1/3으로 표현하고 중성자는 0q=2-1-1/3으로 표현할 것이다. 그러면 이제 1q는 양성자, 0q는 중성자이다. 이들은 이제부터 내가 oms이론에서 사용하기에 이해하기 편하자고 양성자(1q), 중성자(0q)로 정의한 기호이다.
그러면 원자핵 vix안에는 1q,0q일때 가장 가변운 원소 수소(H)이다. 자세히 표현하면 수소의 기본정보는 1q_1,0q_0이다. 여기에 동위원소가 존재하니, 1q_1,0q_1는 중수소이다. 삼중수소는 1q_1,0q_2이다. 굿굳! 그러면 만약에 100중 수소가 존재한다면 1q_0q_100-1인겨. 허허. 나의 oms이론에서의 동위원소는 거의 무한대이니 우리 우주에 존재하지 않는 동위원소도 다른 우주(다중우주)에 존재한다는 전제가 있다. 쩌어업!
그러면 수성에서의 철은 주기율표 8족에 속하는 원소의 하나로, 원소기호 Fe, 원자번호 26, 원자량 55.847(56Fe)이다. 그러면 중성자 수는 원자량(Fe^56 )-양성자 수(원자번호26)=30개 이다.
그러면 나의 1q,0q의 표현법으로 철의 원자량(56Fe)은 1q_26,0q_30=56Fe 이다. 이들이 동위원소를 1q_26,0q_19~46=최소 45Fe ~최대72Fe 동위원소를 자연계에서 가진다. 물론 나의 oms이론에서는 중성자(n)의 수는 무제한적으로 보태기가 가능하니, 최저 26(0)Fe~26(∞)Fe가 나의 1q,0q표기법으로 (1q_26,0q_0)~(1q_26~0q_∞)으로 표현된다. 허허.
그래서 수성의 대기의 상하부의 원소분포들도 나의 oms이론의 표기법으로 보면 원소들의 크고작은 원자량에 따라 얼마든지 왼쪽과 오른쪽으로 몰리는 원자량 크기에 따라 수성의 자연상태를 해석할 수 있다는 주장이다. 허허.
Sample 1.oms (standard)
b0acfd 0000e0
000ac0 f00bde
0c0fab 000e0d
e00d0c 0b0fa0
f000e0 b0dac0
d0f000 cae0b0
0b000f 0ead0c
0deb00 ac000f
ced0ba 00f000
a0b00e 0dc0f0
0ace00 df000b
0f00d0 e0bc0a
Sample 1.2 quasi oms (standard)
0100000010=0,2
0010000100
0001000001
0010001000
0001010000
0000100100
0000100010
2000000000
0000001001
sample 2. oss(standard)
zxdxybzyz
zxdzxezxz
xxbyyxzzx
zybzzfxzy
cadccbcdc
cdbdcbdbb
xzezxdyyx
zxezybzyy
bddbcbdca

- Rock-forming elements such as silicon, sodium or iron, which are relatively nonvolatile, can exist as gases such as silicon monoxide (SiO) only at very high temperatures thought to have existed in early magma oceans. The difference between volatile and non-volatile gas species is that at a given temperature, volatile species have a much greater equilibrium vapor pressure than non-volatile gases. This is the pressure exerted by the atmosphere on the surface of the atmosphere-magma when the two coexist.
-The research team ran an intra-atmospheric coupling model to determine the effects of evaporation from the ocean to the atmosphere, account for the chemical and physical processes in the atmosphere, and then determine the mass loss from the atmosphere to space or back to the planet. Meanwhile, the planet was cooling. Liquid magma begins to crystallize at 1,700 K (2,600 degrees Fahrenheit), so the 1,500 K that Jäggi uses provides a good approximation of the surface melting lifetime and sets the endpoint for mass loss originating from Mercury's magma oceans. In both volatile and non-volatile cases, magma oceans evaporate and feed into the atmosphere.
-Molecules can escape the atmosphere in one of four ways. Plasma heating in the solar wind of charged particles; Photoevaporation of atmospheric species from extremely high-energy solar photons, such as X-rays and ultraviolet photons, is photons from the sun deep in the upper atmosphere that produce an outflow of gases (also known as hydrodynamic escape). Jeans especially escape where high-altitude, high-velocity, low-mass molecules are pushed from the top of the atmosphere before encountering another molecular collision.
Iron (鐵, English: Iron) is a chemical element with the symbol Fe (←Latin: Ferrum) and the atomic number 26. Iron is the final element produced by nuclear fusion and is the heaviest element that does not require catastrophic events such as supernovae. Therefore, it is the most prevalent heavy metal in the universe. In addition, iron is one of the most used metals by mankind, and since it is used in many fields such as vehicles, ships, aircraft, houses, artificial skeletons, and various daily necessities, iron is an important metal indispensable to mankind.
Material 1.
Iron or iron is a chemical element with the symbol Fe and atomic number 26. Iron is the final element produced by nuclear fusion and is the heaviest element that does not require catastrophic events such as supernovae. Therefore, it is the most prevalent heavy metal in the universe. In addition, iron is one of the most used metals by mankind, and since it is used in many fields such as vehicles, ships, aircraft, houses, artificial skeletons, and various daily necessities, iron is an important metal indispensable to mankind. Stable iron isotopes that exist in nature include 54Fe, 56Fe, 57Fe, and 58Fe.
54Fe accounts for 5.8% in nature.
56Fe is the most abundant isotope among iron isotopes that exist in nature.
During the stellar nuclear fusion process, that is, silicon combustion, 28Si undergoes several helium fusion processes to finally form 56Fe. However, some 56Fe forms 60Zn, but since this process absorbs energy, it is formed in a very small amount during nuclear fusion. Therefore, 56Fe is the most abundant isotope among iron isotopes as the final element in the helium fusion process started from 28Si.
57Fe is finally formed from 29Si through several helium fusion processes.
58Fe has the highest internuclear binding energy among iron isotopes, so it is the most stable isotope among iron isotopes, but only exists in a small amount (0.28%).
Starting from 26Al of nuclear fusion, 54Co is finally produced through the helium fusion process in the 30P process, so most 58Fe is produced through the R-process, a neutron capture process in a supernova explosion.
60Fe is an isotope that has a very short half-life of 2.62 million years and does not exist in the natural world at present, but was very abundant on Earth in the past and played a role in maintaining the lava sea for a long time.
60Ni, an element abundantly present on Earth, was formed through beta decay of 60Fe. 60Zn is formed only by absorbing energy rather than emitting energy than 56Ni during the fusion process, so only a very small amount of 60Zn is formed in the fusion process. From this, it can be seen that most of the 60Ni on Earth is an element formed through beta decay of 60Fe, and 60Fe was formed through the R-process of a supernova explosion that occurred during the eventual process of a giant star. Thus, 60Fe is an isotope that occupied a very important part in the early history of the solar system.
https://en.wikipedia.org/wiki/%EC%B2%A0_%EB%8F%99%EC%9C%84_%EC%9B%90%EC%86%8C
=====================
Memo 2112261522 My thought experiment oms storytelling
For an element the oms theory will be used to classify the volatile and nonvolatile or light and heavy of the element in terms of the viger quark field oms for the vix nucleus.
Light elements have fewer protons and neutrons. This means that heavier elements have relatively more protons and neutrons. Here, the proton will be expressed as 1q=22-1/3 and the neutron will be expressed as 0q=2-1-1/3. So now 1q is a proton and 0q is a neutron. From now on, these are the symbols I have defined as protons (1q) and neutrons (0q) to make it easier to understand for use in oms theory.
Then, in the nucleus vix, the most variable element hydrogen (H) is 1q, 0q. In more detail, the basic information of hydrogen is 1q_1,0q_0. There are isotopes here, so 1q_1,0q_1 is deuterium. Tritium is 1q_1,0q_2. good good! Then, if 100 deuterium exists, 1q_0q_100-1 is preferred. haha. Since the isotopes in my oms theory are almost infinite, there is a premise that isotopes that do not exist in our universe also exist in other universes (multiverses). Wow!
Then, iron in Mercury is one of the elements belonging to group 8 of the periodic table, and has the element symbol Fe, atomic number 26, and atomic weight 55.847 (56Fe). Then, the number of neutrons is atomic weight (Fe^56) - number of protons (atomic number 26) = 30.
Then, in my expression of 1q,0q, the atomic weight of iron (56Fe) is 1q_26,0q_30=56Fe. They have isotopes of 1q_26,0q_19~46=minimum 45Fe~maximum 72Fe in nature. Of course, in my oms theory, an unlimited number of neutrons (n) can be added, so the minimum 26(0)Fe~26(∞)Fe is my 1q,0q notation (1q_26,0q_0)~(1q_26~0q_∞) ) is expressed as haha.
Therefore, it is argued that the distribution of elements in the upper and lower parts of Mercury's atmosphere can also be interpreted in terms of the notation of my oms theory. haha.
Sample 1.oms (standard)
b0acfd 0000e0
000ac0 f00bde
0c0fab 000e0d
e00d0c 0b0fa0
f000e0 b0dac0
d0f000 cae0b0
0b000f 0ead0c
0deb00 ac000f
ced0ba 00f000
a0b00e 0dc0f0
0ace00 df000b
0f00d0 e0bc0a
Sample 1.2 quasi oms (standard)
0100000010=0,2
0010000100
0001000001
0010001000
0001010000
0000100100
0000100010
2000000000
0000001001
sample 2. oss(standard)
zxdxybzyz
zxdzxezxz
xxbyyxzzx
zybzzfxzy
cadccbcdc
cdbdcbdbb
xzezxdyyx
zxezybzyy
bddbcbdca
.The mystery of the small dimensionless number with a big effect
큰 효과가 있는 작은 무차원수의 미스터리

앤드류 브래그, 듀크 대학교 크레딧: 듀크 대학교, DECEMBER 23, 2021
-무차원 숫자는 실험실의 과학자들에게만 사용되는 무섭고 이해할 수 없는 용어처럼 들릴 수 있지만, 당신은 알고 있는 것보다 더 많은 경험을 가지고 있습니다. 마하 수는 음속을 기준으로 물체의 속도를 측정하므로 초당 킬로미터 단위로 측정하든 시간당 마일 단위로 측정하든 마하 2는 항상 음속의 두 배입니다.
-COVID-19 대유행이 여전히 전 세계적으로 확산되고 있는 상황에서 R0는 며칠이든 몇 주이든 몇 달이든 간에 질병이 진행되는 동안 얼마나 많은 사람들을 감염시킬 것인지를 측정하는 뉴스에서 지속적으로 중요한 숫자입니다. 물리학, 응용 수학 및 공학에서 무차원 숫자는 매우 중요합니다.
-연구원은 시스템에서 경쟁 효과의 상대적인 강점을 정량화하는 데 사용합니다. 예를 들어, 유체 역학에서 레이놀즈 수는 파이프 흐름에서 점성과 관성력의 상대적 강도를 정량화하는 데 사용됩니다. 밀도와 속도의 단위에 관계없이 값이 약 2300보다 작으면 흐름이 부드럽고 규칙적이며, 4000보다 크면 흐름이 난류이고 혼란스럽습니다.
최근에 노틀담 대학과 트벤테 대학의 동료들과 함께 대기 경계층에서 입자 이동 문제를 조사했습니다. 이 공기 영역은 대기의 가장 낮은 부분이며 지구 표면과의 접촉은 행동에 직접적인 영향을 미칩니다. 휘젓는 방법을 제어하는 물리학은 구름 형성 및 복사 균형과 같은 대기 과정에서의 역할과 대기 질 및 인간 건강에 대한 영향으로 인해 매우 중요합니다. 두 가지 상충되는 효과가 이 영역에서 입자의 수직 운동과 집중을 결정합니다.
-중력은 입자를 지면으로 끌어내리고, 난기류는 입자를 들어올릴 수 있는 항력을 생성합니다. 연구자들은 종종 이러한 경쟁 효과를 무차원 침강 수 Sv로 정량화합니다. 이는 난류가 없을 때 입자가 얼마나 빨리 침강하는지와 표면 근처의 난류 기류의 특성 속도 사이의 비율입니다. 일반적인 지혜는 Sv가 매우 크면 입자 운동에 대한 난류의 영향을 무시할 수 있는 반면 Sv가 매우 작으면 중력 침강의 영향을 무시할 수 있다는 것입니다. 최근 논문에서 수치 시뮬레이션 결과 매우 놀라운 사실이 밝혀졌습니다. 중력 침강은 Sv가 매우 작은 경우에도 난류 경계층의 입자 농도 프로파일에 강하게 영향을 미쳤습니다. 이 당혹스러운 결과는 기존의 통념에 어긋나는 것 입니다. 강도를 정량화하는 무차원 숫자가 매우 작을 때 입자 농도에 대한 중력의 영향이 어떻게 매우 강할 수 있습니까? 우리는 이 놀라운 결과를 설명할 방법을 찾아야 했습니다.
-이를 위해 위상 공간 확률 밀도 함수 방법을 사용하여 입자 농도에 대한 정확한 수학 방정식을 구성했습니다. 이 정확한 결과에 따르면 서로 다른 물리적 메커니즘 간의 경쟁이 입자 농도를 결정하며 그 중 하나만 Sv에 비례합니다. 그런 다음 우리는 방정식에 대해 점근적 분석을 수행했으며 분석은 농도 방정식의 다른 메커니즘이 대기 경계층의 특정 영역에서 Sv에 비해 작아지는 방식으로 높이에 의존한다는 것을 보여주었습니다. 따라서 Sv가 매우 작더라도 흐름의 특정 영역에서 농도 방정식의 다른 요인보다 훨씬 클 수 있습니다. 실제로 분석에 따르면 Sv가 아무리 작더라도 0이 아닌 한 대기 경계층에는 그 영향을 무시할 수 없는 영역이 항상 존재합니다.
이것은 수치 시뮬레이션의 당혹스러운 결과를 설명했습니다. 이 놀라운 결과에서 파생되는 중요한 의미가 있습니다. 첫째, 거의 모든 이전 연구는 Sv가 작은 영역을 고려할 때 입자 농도에 대한 침전 효과를 무시했으며 우리 결과는 이것이 매우 큰 오류로 이어질 수 있음을 보여줍니다. 따라서 이러한 연구와 결론을 재검토할 필요가 있습니다. 둘째, 더 일반적으로 물리적 시스템에서 무차원 숫자의 의미와 의미를 해석할 때 매우 주의해야 합니다. 우리의 결과는 어떤 경우에는 시스템에서 특정 효과의 중요성을 수량화하기 위해 무차원 숫자를 사용하는 것이 매우 오도될 수 있고 세심한 주의가 필요함을 보여줍니다. 이 작업은 Physical Review Fluids에 게시되었습니다 .
추가 탐색 충격파의 현상을 시뮬레이션하는 새로운 모델 추가 정보: AD Bragg et al, 침강 매개변수가 점근적으로 작은 경우에도 침강은 벽 경계 난류 흐름에서 입자 농도를 강력하게 수정합니다. Physical Review Fluids (2021). DOI: 10.1103/PhysRevFluids.6.124301 듀크대학교 제공
https://phys.org/news/2021-12-mystery-small-dimensionless-big-effect.html
==================
메모 2112261651 나의 사고실험 oms스토리텔링
나의 oms이론에서는 하찮은 숫자나 입자 하나도 전체에 참여하는 존재이라는 점이다. 그런데 d구조의 특정 위치에 있으면 아무리 큰 수이라도 전체에 영향을 미치지 않고 이동할 수 있다는 것이다.
이는 하찮게 보이는 보이는 수많은 입자들이 그룹을 이루면 커다란 힘을 발휘하고 소규모일찌라도 밀도가 높으면 힘을 가질 수 있는 무차원에 속한 것들이 다양하게 차원을 가진 시스템처럼 영향을 준다. 이는 샘플1.2 특이점(smola 2의 값)이 전체(vix system)에 영향을 준다는 점이다. 허허.
Sample 1.oms (standard)
b0acfd 0000e0
000ac0 f00bde
0c0fab 000e0d
e00d0c 0b0fa0
f000e0 b0dac0
d0f000 cae0b0
0b000f 0ead0c
0deb00 ac000f
ced0ba 00f000
a0b00e 0dc0f0
0ace00 df000b
0f00d0 e0bc0a
Sample 1.2 quasi oms (standard)
0100000010=0,2
0010000100
0001000001
0010001000
0001010000
0000100100
0000100010
2000000000
0000001001
sample 2. oss(standard)
zxdxybzyz
zxdzxezxz
xxbyyxzzx
zybzzfxzy
cadccbcdc
cdbdcbdbb
xzezxdyyx
zxezybzyy
bddbcbdca

-Dimensionless numbers may sound like a scary and incomprehensible term used only by scientists in the lab, but you have more experience than you know. Mach number measures the speed of an object relative to the speed of sound, so Mach 2 is always twice the speed of sound, whether measured in kilometers per second or miles per hour.
- With the COVID-19 pandemic still spreading across the globe, R0 continues to be an important number in the news, measuring how many people it will infect during the course of the disease, whether it be days, weeks or months. Dimensionless numbers are very important in physics, applied mathematics and engineering.
-Gravity pulls the particles down to the ground, and turbulence creates a drag force that can lift the particles up. Researchers often quantify these competitive effects as dimensionless sedimentation water Sv. It is the ratio between how quickly particles settle in the absence of turbulence and the characteristic velocity of a turbulent airflow near the surface. The general wisdom is that when Sv is very large, the effect of turbulence on particle motion is negligible, whereas when Sv is very small, the effect of gravitational sedimentation is negligible. In a recent paper, numerical simulations revealed very surprising facts. Gravity sedimentation strongly influenced the particle concentration profile of the turbulent boundary layer even when the Sv was very small. This embarrassing result goes against conventional wisdom. How can the effect of gravity on particle concentration be so strong when the dimensionless number quantifying intensity is so small? We had to find a way to explain this surprising result.
- For this, an exact mathematical equation for particle concentration was constructed using the phase-space probability density function method. These precise results show that competition between different physical mechanisms determines particle concentration, only one of which is proportional to Sv. We then performed an asymptotic analysis of the equation, and the analysis showed that other mechanisms of the concentration equation depend on the height in a certain region of the atmospheric boundary layer in such a way that it becomes small relative to Sv. So even if Sv is very small, it can be much larger than the other factors in the concentration equation in certain regions of the flow. Indeed, analysis shows that no matter how small the Sv is, there is always a region in the atmospheric boundary layer where the effect cannot be neglected, unless it is zero.
=====================
Memo 2112261651 My thought experiment oms storytelling
In my oms theory, every insignificant number or particle participates in the whole. However, if it is at a specific location in the d structure, no matter how large the number, it can move without affecting the whole.
This affects like a system with multiple dimensions of non-dimensional objects that can exert a great force when a large number of seemingly insignificant particles form a group, and have a force even if they are small and dense. This is that the sample 1.2 singularity (value of smola 2) affects the whole (vix system). haha.
Sample 1.oms (standard)
b0acfd 0000e0
000ac0 f00bde
0c0fab 000e0d
e00d0c 0b0fa0
f000e0 b0dac0
d0f000 cae0b0
0b000f 0ead0c
0deb00 ac000f
ced0ba 00f000
a0b00e 0dc0f0
0ace00 df000b
0f00d0 e0bc0a
Sample 1.2 quasi oms (standard)
0100000010=0,2
0010000100
0001000001
0010001000
0001010000
0000100100
0000100010
2000000000
0000001001
sample 2. oss(standard)
zxdxybzyz
zxdzxezxz
xxbyyxzzx
zybzzfxzy
cadccbcdc
cdbdcbdbb
xzezxdyyx
zxezybzyy
bddbcbdca
댓글