.Strange Quasiparticles – Called Anyons – May Be Useful in Future Quantum Computers
http://blog.naver.com/mssoms
http://jl0620.blogspot.com
http://jk0620.tripod.com
https://www.facebook.com/junggoo.lee.9

.Strange Quasiparticles – Called Anyons – May Be Useful in Future Quantum Computers
이상한 준입자 – Anyons – 미래 양자 컴퓨터에 유용할 수 있음

주제:브라운 대학교입자 물리학양자 컴퓨팅 으로 브라운 대학 2021년 11월 12일 Anyons 이상한 입자
연구원들은 Anyons라고 불리는 비순응 입자를 탐지하기 위한 새로운 전략을 보여줍니다 임의의 이상한 입자가 열을 발산하는 방법을 관찰함으로써 연구자들은 위상 양자 컴퓨팅 과 관련될 수 있는 시스템에서 이러한 입자의 특성을 조사할 수 있음을 보여주었습니다 .
브라운 대학 연구원 팀은 미래 양자 컴퓨터에 유용할 수 있는 이상한 준입자인 임의의 성질을 조사하는 새로운 방법을 보여주었습니다. Physical Review Letters 저널에 발표된 연구 에서 팀은 열을 전도하는 방식의 미묘한 특성을 측정하여 사람을 조사하는 방법을 설명합니다.
다른 방법은 전하를 사용하여 이러한 입자를 조사하는 반면, 이 새로운 방법을 사용하면 연구원들이 비전도성 물질에서도 아무 것도 조사할 수 있습니다. 연구원들은 비전도성 시스템이 훨씬 덜 엄격한 온도 요구 사항을 가지고 있어 양자 컴퓨팅을 위한 보다 실용적인 옵션이 되기 때문에 이것이 중요하다고 말합니다. 브라운 대학의 물리학 교수인 디마 펠드만(Dima Feldman)은 “우리는 전하를 사용하여 모든 사람을 조사할 수 있는 아름다운 방법을 가지고 있지만, 문제는 위상 양자 컴퓨팅으로 알려진 것에 유용한 절연 시스템에서 이들을 어떻게 감지하는가 하는 것”이라고 말했습니다.
-작가. "우리는 열전도율을 사용하여 수행할 수 있음을 보여줍니다. 본질적으로 이것은 물질의 모든 상태에서 작동하는 모든 사람을 위한 보편적인 테스트입니다.” 누구나 관심을 갖는 이유는 일상의 3차원 세계에서 입자와 동일한 규칙을 따르지 않기 때문입니다. 3차원에서 입자의 종류는 크게 보손(boson)과 페르미온(fermion)뿐입니다. 보손은 보스-아인슈타인 통계로 알려진 것을 따르고 페르미온은 페르미-디랙 통계를 따릅니다. 일반적으로 말해서, 이러한 다양한 통계적 규칙은 양자 시스템에서 한 보존자가 다른 보존자 주위를 도는 경우 입자의 파동 함수(양자 상태를 완전히 설명하는 방정식)가 변경되지 않는다는 것을 의미합니다.
-반면에 페르미온이 다른 페르미온 주위를 도는 경우 파동 함수의 위상 값은 양의 정수에서 음의 정수로 바뀝니다. 다시 궤도를 도는 경우 파동 함수는 원래 상태로 돌아갑니다. 2차원에 국한된 시스템에서만 나타나는 Anyons는 두 가지 규칙 중 어느 것도 따르지 않습니다.
임의의 임의가 다른 임의의 궤도를 도는 경우 파동 함수는 정수의 일부만 변경됩니다. 그리고 다른 궤도가 반드시 파동 함수의 원래 값을 복원하는 것은 아닙니다. 대신, 마치 파티클이 시작 위치로 돌아가더라도 다른 파티클과의 상호 작용에 대한 "기억"을 유지하는 것처럼 새로운 값을 갖습니다. 과거 상호 작용에 대한 기억은 강력한 방식으로 정보를 인코딩하는 데 사용할 수 있습니다. 이것이 입자가 양자 컴퓨팅에 흥미로운 도구인 이유입니다.
양자 컴퓨터는 오늘날의 컴퓨터에서는 거의 불가능한 특정 유형의 계산을 수행할 것을 약속합니다. 토폴로지 양자 컴퓨터로 알려진 anyons를 사용하는 양자 컴퓨터는 사용 가능한 양자 컴퓨터를 찾는 데 큰 걸림돌인 정교한 오류 수정 없이 작동할 가능성이 있습니다. 그러나 컴퓨팅에 anyons를 사용하려면 먼저 양자 통계를 조사하여 이러한 입자를 식별할 수 있어야 합니다. 작년에 연구원들은 전하 간섭계로 알려진 기술을 사용하여 처음으로 이를 수행했습니다.
-본질적으로, anyons는 서로를 중심으로 회전하여 파동 기능이 때때로 서로 간섭하게 만듭니다. 간섭 패턴은 입자의 양자 통계를 나타냅니다. 전하를 사용하여 누구를 조사하는 기술은 전기를 전도하는 시스템에서 아름답게 작동하지만 비전도 시스템에서 누구를 조사하는 데는 사용할 수 없다고 연구원들은 말합니다. 그리고 비전도성 시스템은 절대 영도에 가까워야 하는 전도성 시스템보다 더 높은 온도에서 유용할 가능성이 있습니다 . 이는 토폴로지 양자 컴퓨팅의 보다 실용적인 옵션이 됩니다.
이 새로운 연구를 위해 2017년 처음으로 모든 사람의 열전도율을 측정 한 팀의 일원이었던 Feldman 은 Brown 대학원생 Zezhu Wei 및 Brown 물리학 교수이자 실험가인 Vesna Mitrovic과 협력했습니다. Wei, Feldman 및 Mitrovic은 매우 특정한 기하학적 구조로 에칭된 2차원 고체의 열전도 특성을 비교하여 해당 시스템의 임의의 통계를 나타낼 수 있음을 보여주었습니다. Mitrovic은 "두 형상에서 열전도율의 차이는 분수 통계에 대한 총기의 증거가 될 것입니다."라고 말했습니다. "이 연구가 수행하는 것은 사람들이 이러한 이상한 통계를 테스트하기 위해 실험실에서 실험을 설정하는 방법을 정확히 보여주는 것입니다." 궁극적으로 연구원들은 이 연구가 토폴로지 양자 컴퓨팅에 실제로 활용될 수 있는지 여부를 이해하는 한 단계가 되기를 희망합니다.
참조: Zezhu Wei, V. F. Mitrović 및 D. E. Feldman의 "회전 액체의 임의의 열 간섭계", 2021년 10월 11일, Physical Review Letters . DOI: 10.1103/PhysRevLett.127.167204 이 연구는 국립과학재단(DMR-1902356, QLCI-1936854, DMR-1905532)의 지원을 받았습니다.
=====================
메모 2111160544 나의 사고실험 oms 스토리텔링
oms이론에서의 준입자는 샘플1.2 quasi oms이다. 준입자는 두개의 불안전한 구조가 중첩된 현상이다. 이들이 양자 컴퓨팅에 유용할 수 있는지는 알 수 없지만 양자의 얽힘을 만들고 있다는 증거는 확실하다. 중요한 사실은 샘플1.2 quasi oms 업버전마다 고유의 준입자 단위가 매우 광범위하게 나타나고 있어 양자 컴퓨팅에 smola_d구조 단위 역시 매우 많을 것으로 보인다.
이들이 중첩하여 중심을 정하여 상호 회전을 하면 다양한 간섭 현상을 보여 물질더미을 인수분해 하여 알수없이 남겨진 덩어리같은 이미징으로 보이게 될 것이다. 허허. 우주에 왜 그처럼 많은 먼지와 가스가 알 수없는 말머리 성운 따위를 만들어냈는지 해답을 줄 수 있다. 허허.
샘플1.oms(standard)
b0acfd 0000e0
000ac0 f00bde
0c0fab 000e0d
e00d0c 0b0fa0
f000e0 b0dac0
d0f000 cae0b0
0b000f 0ead0c
0deb00 ac000f
ced0ba 00f000
a0b00e 0dc0f0
0ace00 df000b
0f00d0 e0bc0a
샘플2. oss
zxdxybzyz
zxdzxezxz
xxbyyxzzx
zybzzfxzy
cadccbcdc
cdbdcbdbb
xzezxdyyx
zxezybzyy
bddbcbdca

-Writer. "We demonstrate that we can be done using thermal conductivity. Essentially this is a universal test for everyone working in all states of the substance." Everyone has a interest because it does not follow the same rules as particles in the three-dimensional world. In the three-dimensional, the type of particles is largely a boson (Boson) and fermion (fermion). Following Fermion follows Fermi - Durrack statistics. In general, these various statistical rules do not change the wave function of particles (equations that completely describe quantum states) if a property is around other prescribers in the quantum system. Means.
- On the other hand, if Fermion is around other femions, the phase value of the wave function changes from the positive integer to the integer. If the orbit again, the wave function returns to its original state. Anyons that appear only on the two-dimensional systems are not following any of the two rules.
- In essence, Anyons rotates around each other to make the wave function interfere with each other. Interference patterns represent quantum statistics of particles. Techniques to investigate who use the charges are beautifully working on the system that conducts electricity, but they are not available in the vision system to investigate anyone. And a non-conductive system is likely to be useful at higher temperatures than a conductive system that must be close to absolute spirit. This is a more practical option of topology quantum computing.
==========================================
Notes 2111160544 My Accident Experiment OMS Story Telling
The quartz in the OMS theory is the sample 1.2 Quasi OMS. The quantity is the phenomenon of two non-safe structures overlapped. It is certain that the evidence that they can be useful for quantum computing, but they are making entanglement of both. The important fact is that the unique quantity unit is very broad, and the SMOLA_D structure unit is also very widely seen for quantum computing.
When they are superimposed, they will be seen as a massive immersion, which is a lump that is left, and a variety of interference phenomena. haha. As far as the universe that makes it possible to make a lot of dust and gas to make a word that you have created. haha.
Sample 1.OMs (Standard)
b0acfd 0000e0
000AC0 F00BDE
0C0Fab 000E0D
E00D0C 0B0FA0
F00E0 B0DAC0
D0F000 CAE0B0
0B000F 0EAD0C
0deb00 AC000f
CED0BA 00F000
A0B00E 0DC0F0
0ACE00 DF000B
0F00D0 E0BC0A
Sample 2. OSS
zxdxybzyz
zxdzxezxz
xxbyyxzzx
zybzzfxzy
CADCCBCDC
cdbdcbdbb
xzezxdyyx
Zxezybzyy
BDDBCBDCA

.Key Witness Helps DOE Scientists Detect “Spooky” Quantum Entanglement in Solid Materials
주요 증인은 DOE 과학자들이 고체 물질에서 "으스스한" 양자 얽힘을 감지하는 데 도움을 줍니다
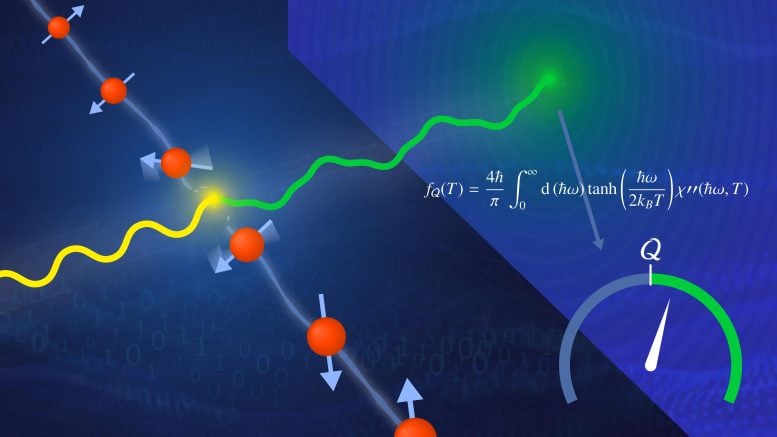
주제:하다재료과학중성자오크리지 국립연구소양자 물리학 으로 오크 리지 국립 연구소 , 2021 11월 14일 양자 피셔 정보 계산 붉은 구체로 묘사된 물질의 스핀은 산란된 중성자에 의해 조사됩니다. 그림의 QFI 계산과 같은 얽힘 목격자를 적용하면 중성자가 일종의 양자 게이지를 형성하게 됩니다. 이 게이지를 통해 연구원들은 고전적 스핀 변동과 양자 스핀 변동을 구별할 수 있습니다. 출처: Nathan Armistead/ORNL, 미국 에너지부 PHYSICS NOVEMBER 14, 2021
양자 얽힘은 두 입자가 물리적 연결 없이 소통하는 것처럼 보일 때 발생하며, 알버트 아인슈타인은 "원거리에서 으스스한 행동"이라고 불렀던 현상입니다. 거의 90년 후, 미국 에너지부의 Oak Ridge 국립 연구소가 이끄는 팀은 양자 물질에서 자성 입자 또는 스핀 사이의 얽힘의 존재를 증명할 수 있는 "양자 얽힘 목격자"의 생존 가능성을 입증했습니다. ORNL, Helmholtz-Zentrum Berlin, 베를린 공과 대학, Laue-Langevin 연구소, Oxford 대학 및 Adam Mickiewicz 대학의 연구원을 포함한 팀은 중성자 산란 실험과 계산 시뮬레이션을 조합하여 3명의 얽힘 목격자를 테스트했습니다.
얽힘 목격자는 고전 영역과 양자 영역 사이의 임계값을 넘는 스핀을 결정하기 위한 데이터 분석 도구 역할을 하는 기술입니다. 1960년대 존 스튜어트 벨(John Stewart Bell)에 의해 처음 소개된 얽힘 목격자들은 다른 과학자들이 질문한 양자 이론이 옳았다는 것을 확인했습니다. Bell의 기술은 한 번에 한 쌍의 입자를 감지하는 데 의존했지만 이 접근 방식은 수조 및 수조 개의 입자로 구성된 고체 물질을 연구하는 데 유용하지 않습니다.
새로운 얽힘 목격자를 사용하여 얽힌 스핀의 대규모 집합을 대상으로 지정하고 감지함으로써 팀은 이 개념을 확장하여 고체 물질을 특성화하고 초전도체 및 양자 자석의 특이한 거동을 연구했습니다. 목격자가 신뢰할 수 있는지 확인하기 위해 팀은 이전 스핀 역학 연구로 인해 얽힌 것으로 알려진 물질에 세 사람 모두를 적용했습니다 . Bell의 접근 방식을 기반으로 한 두 증인은 이 1차원 스핀 체인(다른 입자를 무시하면서 이웃과 통신하는 인접한 스핀의 직선)에 얽힘의 존재를 적절하게 지적했지만 세 번째는 다음을 기반으로 합니다.
양자 정보 이론은 동일한 작업에서 예외적으로 잘 수행되었습니다. ORNL의 박사후 연구원이자 팀 증명의 주저자인 Allen Scheie는 "양자 피셔 정보(QFI) 증인은 이론과 실험이 밀접하게 중첩되어 얽힘을 정량화할 수 있는 강력하고 신뢰할 수 있는 방법입니다"라고 말했습니다. Physical Review B에 발표된 개념 논문 . 자연에서 양자로 보이는 물질의 변동은 온도 규모의 절대 영도 에서만 사라지는 임의의 열 운동에 의해 발생할 수 있기 때문에 대부분의 현대적인 방법은 이러한 잘못된 경보와 실제 양자 활동을 구별할 수 없습니다.
연구팀은 2016년 이 기술이 제안된 이후 가장 포괄적인 QFI 시연의 일환으로 온도가 감소함에 따라 얽힘이 증가한다는 이론적 예측을 확인했을 뿐만 아니라 고전 활동과 양자 활동을 성공적으로 구별했습니다. 양자 과학 센터(QSC)의 양자 자석에 초점을 맞춘 프로젝트를 이끄는 ORNL 중성자 산란 과학자 앨런 테넌트(Alan Tennant)는 "가장 흥미로운 물질은 양자 얽힘으로 가득 차 있지만 정확히 계산하기 가장 어려운 물질"이라고 말했다. ORNL에 본부를 둔 DOE 국립 양자 정보 과학 연구 센터. 이전에는 양자 물질을 신속하게 식별하는 문제가 양자 정보 과학 분야를 발전시키면서 새로운 장치와 센서를 개발하기 위해 얽힘을 이용하는 것을 포함하는 센터의 임무에 중대한 장애물을 제시했습니다. QFI를 사용하여 이 프로세스를 간소화함으로써 QSC 연구원들은 데이터 저장 및 컴퓨팅 애플리케이션을 위한 초전도체라고 하는 전기에 저항하지 않는 물질 및 양자 스핀 액체라고 하는 희귀 상 물질과 같은 물질의 힘을 활용하는 데 집중할 수 있습니다.
"QFI의 힘은 과학자들이 불확실성을 줄이고 극도로 정확한 측정값을 얻기 위해 여러 개의 준입자를 얽히게 하는 양자 계측과의 연결에서 비롯됩니다."라고 Scheie가 말했습니다. “QFI 증인은 기존 측정의 정밀도를 사용하여 각 스핀이 얽혀 있는 최소 입자 수를 결정함으로써 이 접근 방식을 뒤집었습니다. 이것은 양자 상호작용을 드러내는 강력한 방법이며, 이는 QFI가 모든 양자 자성 물질에 실제로 적용할 수 있음을 의미합니다." QFI가 재료를 올바르게 분류할 수 있다는 것을 확인한 팀은 스핀이 무작위로 회전하지 않고 평면에 놓이게 하는 특성인 이방성을 특징으로 하는 보다 복잡한 재료인 두 번째 1차원 스핀 체인을 테스트했습니다.
연구진은 스핀 사슬에 자기장을 가해 얽힘 전이를 관찰했으며, 얽힘의 양이 다시 나타나기 전에 0으로 떨어졌습니다. 그들은 이 발견을 Physical Review Letters 에 발표했습니다 . 이러한 결과를 달성하기 위해 연구원들은 중성자 산란을 사용하여 두 스핀 사슬을 연구한 다음 수십 년 전에 영국의 ISIS Neutron Source와 프랑스의 Laue-Langevin 연구소에서 수행한 실험의 기존 데이터와 광각 범위 초퍼의 새로운 데이터를 분석했습니다. ORNL이 운영하는 DOE Office of Science 사용자 시설인 Spallation Neutron Source에 위치한 분광계. 그들은 또한 이상적인 이론적 데이터에 대해 결과를 검증하기 위해 보완적인 시뮬레이션을 실행했습니다.
Tennant가 "아름다운 단순함"이라고 설명하는 중성자는 중성 전하와 비파괴 특성 때문에 재료의 특성을 조사하는 데 이상적인 도구입니다. “에너지를 전달하는 시료에서 산란되는 중성자의 분포를 연구함으로써 우리는 이론에 의존하지 않고 아직 존재하지 않는 거대한 양자 컴퓨터가 필요 없이 중성자를 게이지로 사용하여 양자 얽힘을 측정할 수 있었습니다. "라고 테넌트가 말했다. 팀에 따르면 고급 계산 및 실험 리소스의 이러한 조합은 원래 양자 역학의 창시자가 질문한 양자 얽힘의 특성에 대한 답변을 제공했습니다. Scheie는 QFI 계산이 결국 가장 신비한 양자 물질을 특성화할 수 있는 중성자 산란 실험의 표준 절차의 일부가 될 것으로 기대합니다.
참조: A. Scheie, Pontus Laurell, AM Samarakoon, B. Lake, SE Nagler, GE Granroth, S. Okamoto, G. Alvarez 및 DA Tennant의 "중성자 산란을 사용한 양자 자석의 얽힘 목격", 2021년 6월 28일, Physical Review B . DOI: 10.1103/PhysRevB.103.224434 Pontus Laurell, Allen Scheie, Chiron J. Mukherjee, Michael M. Koza, Mechtild Enderle, Zbigniew Tylczynski, Satoshi Okamoto, Radu Coldea, D. Alan Tennant의 " 양자 자석 Cs 2 CoCl 4의 얽힘 정량화 및 제어 " Alvarez, 2021년 7월 13일, Physical Review Letters . DOI: 10.1103/PhysRevLett.127.037201 연구원들은 DOE Office of Science, DOE의 Scientific Discovery through Advanced Computing 프로그램, QSC, ORNL의 연구실 주도 연구 및 개발 프로그램, ORNL에 위치한 DOE Office of Science 사용자 시설인 Center for Nanophase Materials Sciences의 지원을 받았습니다. 유럽 연합 Horizon 2020 연구 및 혁신 프로그램의 유럽 연구 위원회.
댓글