.Venus’ Geological Secrets Revealed Through “Pack Ice” Tectonics
http://blog.naver.com/mssoms
http://jl0620.blogspot.com
http://jk0620.tripod.com
https://www.facebook.com/junggoo.lee.9

.Venus’ Geological Secrets Revealed Through “Pack Ice” Tectonics
금성의 지질 학적 비밀은“갑 얼음”구조론을 통해 밝혀졌다

주제 :노스 캐롤라이나 주립대 학교행성지질 구조 판금성 으로 노스 캐롤라이나 주립 대학 2021년 6월 21일 라비니아 플라 니티 아 금성의 저지대 지역 중 하나 인 Lavinia Planitia의 폭 1,100km, 암석권이 지각 구조의 벨트 (노란색)로 구분 된 블록 (보라색)으로 조각난 곳입니다. 출처 : NASA / JPL 원본 이미지를 기반으로 한 NC State University
금성의 표면에 대한 새로운 분석은 깨진 얼음 덩어리처럼 서로 부딪친 지각 블록 형태의 지각 운동의 증거를 보여줍니다. 이 블록들의 움직임은 금성이 여전히 지질 학적으로 활동하고 있음을 나타내며 과학자들에게 외계 행성 구조론과 지구에서 가장 초기의 지각 활동에 대한 통찰력을 제공 할 수 있습니다.
노스 캐롤라이나 주립 대학의 행성 과학 부교수이자 공동 교신 저자 인 폴 번 (Paul Byrne)은“우리는 금성에서 이전에 인식되지 않았던 지각 변형 패턴을 확인했습니다.이 패턴은 지구와 같이 내부 운동에 의해 구동됩니다.
작품. "현재 지구에서 볼 수있는 구조론과는 다르지만, 여전히 행성 표면에서 내부 운동이 표현되고 있다는 증거입니다." 금성은 화성이나 지구의 달처럼 움직이지 않는 단단한 외피 또는 암석권을 가지고 있다고 오랫동안 가정했기 때문에이 발견은 중요합니다. 대조적으로, 지구의 암석권은 지각판으로 쪼개져 뜨겁고 약한 맨틀 층 위에 서로 마주 보거나 떨어져서 아래로 미끄러집니다.
Byrne과 국제 연구원 그룹은 NASA의 Magellan 임무에서 얻은 레이더 이미지를 사용하여 금성의 표면을 매핑했습니다. 행성 표면의 대부분을 구성하는 광활한 금성의 저지대를 조사 할 때 암석권의 큰 블록이 움직이는 것처럼 보이는 영역을 보았습니다. 얼어 붙은 호수 위로 부서진 뭉치 얼음처럼 서로를 잡아 당기고, 함께 밀고, 회전하고, 미끄러지는 것처럼 보입니다. . 연구팀은이 변형의 컴퓨터 모델을 만들었고, 행성 내부의 느린 움직임이 표면에서 보이는 구조론의 스타일을 설명 할 수 있음을 발견했습니다. "이러한 관찰은 지구에서 일어나는 것과 유사한 방식으로 내부 운동이 금성의 표면 변형을 주도하고 있음을 알려줍니다."라고 Byrne은 말합니다.
“지구의 판 구조론은 맨틀의 대류에 의해 구동됩니다. 맨틀은 다른 곳에서 뜨겁거나 차갑고, 움직이며, 그 움직임 중 일부는 판 움직임의 형태로 지구 표면으로 전달됩니다. “그 테마에 대한 변형이 금성에서도 펼쳐지는 것 같습니다. 이것은 지구와 같은 판 구조론이 아닙니다. 여기에는 거대한 산맥이나 거대한 섭입 시스템이 생성되지 않습니다. 그러나 이는 이전에 전 세계적으로 입증 된 적이없는 내부 맨틀 흐름으로 인한 변형의 증거입니다.” 이러한 지각 블록과 관련된 변형은 금성이 여전히 지질 학적으로 활성 상태임을 나타낼 수 있습니다. "우리는 금성의 상당 부분이 시간이 지남에 따라 화산으로 재 포장 되었기 때문에 지구의 일부 지역은 지질 학적으로 말하면 정말 젊을 수 있습니다."라고 Byrne은 말합니다.
-“그러나이 어린 용암 평원에서 여러 개의 밀집된 블록이 형성되어 변형되었습니다. 이는 평원이 깔린 후 암석권이 조각난 것을 의미합니다. 이것은 우리에게 이러한 블록 중 일부가 지질 학적으로 매우 최근에 이동했을 수 있다고 생각할 이유를 제공합니다. 아마도 오늘날까지도 마찬가지입니다.” 연구자들은 금성의 새로 인식 된“갑 얼음”패턴이 우리 태양계 밖의 행성과 훨씬 더 젊은 지구에서 지각 변형을 이해하는 데 단서를 제공 할 수 있다고 낙관합니다. “행성의 암석권의 두께는 주로 내부와 표면의 온도에 따라 달라집니다.”라고 Byrne은 말합니다.
“젊은 지구 내부의 열 흐름은 지금보다 최대 3 배 더 컸기 때문에 암석권은 오늘날 금성에서 볼 수있는 것과 유사했을 수 있습니다. 밀고 당기고 밀치는 블록.” NASA와 유럽 우주국은 최근 Magellan보다 훨씬 높은 해상도로 행성 표면의 관측을 획득 할 금성에 대한 3 개의 새로운 우주선 임무를 승인했습니다. "금성 탐사에 대한 새로운 관심을 보게되어 기쁩니다. 특히이 임무가 행성의 저지대가 지각 블록으로 쪼개 졌다는 우리의 주요 발견을 테스트 할 수있게되어 매우 기쁩니다."라고 Byrne은 말합니다.
이 작품 은 국립 과학 아카데미 회보에 나타납니다 . Columbia University의 Sean Solomon은 공동 교신 저자입니다. 서리 런던 대학교의 리처드 게일; 이스탄불 공과 대학의 AM Celâl Sengör; Baylor University의 Peter James; 그리고 조지아 대학교의 Christian Klimczak도이 작업에 기여했습니다. 참조 : "금성의 세계적으로 조각난 이동 암석권"2021 년 6 월 21 일 , 국립 과학 아카데미 회보 저자 : 폴 K. 번, 노스 캐롤라이나 주립대 학교; Richard C. Ghail, University of London, Surrey; AM Celâl Sengör, Istanbul Technical University; Peter B. James, Baylor University; 조지아 대학교의 Christian Klimczak; 컬럼비아 대학교 Sean C. Solomon
요약: 금성은 지구를 특징 짓는 이동식 지각판의 모자이크와는 대조적으로 전 세계적으로 연속적인 암석권을 소유 한 것으로 여겨져 왔습니다. 그러나 금성 표면은 광범위하게 변형되었으며, 아마도 저 강도 하부 지각과 함께 작용하는 밑에있는 맨틀의 대류가 일부 표면 수평 변형의 원인으로 제안되었습니다. 그러나 맨틀 대류에 의한 금성의 표면 이동 정도와 그 구조적 표현의 스타일과 규모는 불분명합니다. 우리는 비너스 저지대에 전 세계적으로 분포 된 지각 블록 집합을보고하며, 이는 밀집 얼음처럼 서로에 대해 회전 및 / 또는 측면으로 이동했다는 증거를 보여줍니다. 금성에 대한 이러한 변형의 적어도 일부는 지역에서 가장 어린 평원 재료의 배치 이후입니다. 장파장 중력 및 지형과 일치하는 내부 점성 유동 모델에서 계산 된 석권 응력은 이러한 블록이 존재하는 모든 영역에서 상부 금성 지각의 취성 파괴를 유발하기에 충분하며, 내부 대류 운동이 변형을 유도하는 메커니즘을 제공 할 수 있음을 확인합니다. 표면. 수성, 달, 화성의 정적 암석권을 나타내는 지각 스타일과 현저한 대조를 이루는 금성의 제한적이지만 널리 퍼진 암석권 이동성은 지구 열유속이 상당히 높았던 초기 지구의 내부 표면 결합과 유사 할 수 있습니다. , 암석권은 일반적으로 오늘날보다 얇습니다.
https://scitechdaily.com/venus-geological-secrets-revealed-through-pack-ice-tectonics/
===메모 2106221743 나의 oms 스토리텔링
금성의 지각의 일부를 보여주는 곳은 화산활동으로 용암이 개천처럼 흐르는 모습이다. 금성의 표면이 물 위의 유빙처럼 서로 부딪히고 밀어내는 지각 덩어리(crustal block) 형태의 구조 운동을 하는 것으로 밝혀졌다.
이런 곳이 금성의 전체는 아닐듯하다. 이미 대륙을 형성하여 2,6킬로의 산과 산맥도 있는 것으로 보인다. 표면 온도가 섭씨 400도에도 고지대의 저온과 저지대의 저온의 사이에는 생명체가 존재할 이상적인 섭씨 30도 미만 온도를 가질 수 있다. 화성과는 달리 온도의 편차가 큰 환경이 그 강력한 이유이다.
Sample 1. 등변oms//는고온과 저온을 조합하여 섭씨 30도을 유지할 수 있다. 섭씨 온도의 환경변화 : (a+b+c)-(d+e+f)=(a+b+c=400도)state-(d200+e100+f70=370도)state = 생명체 최적온도 30도 state.
금성의 밤낮의 기온차로 고온의 환경이 몇단계 순차적으로 저온으로 다운이 되면 섭씨 400도에서 섭씨 30도로 다운 시킬 수 있다.
Sample 1. 등변oms//
b0acfd 0000e0
000ac0 f00bde
0c0fab 000e0d
e00d0c 0b0fa0
f000e0 b0dac0
d0f000 cae0b0
0b000f 0ead0c
0deb00 ac000f
ced0ba 00f000
a0b00e 0dc0f0
0ace00 df000b
0f00d0 e0bc0a

-“But in this young lava plain several dense blocks formed and transformed. This means that the lithosphere is fragmented after the plain has been laid. This gives us reason to think that some of these blocks may have moved geologically very recently. Perhaps even today.” Researchers are optimistic that Venus' newly recognized “carp-ice” pattern may provide clues to understanding tectonic deformations on planets outside our solar system and on a much younger Earth. “The thickness of a planet's lithosphere depends primarily on the temperature inside and on the surface,” says Byrne.
=== memo 2106221743 my oms storytelling
Part of the crust of Venus is shown where lava flows like streams due to volcanic activity. It has been found that the surface of Venus undergoes tectonic movements in the form of crustal blocks that collide and push against each other like drift ice on water.
It seems that this place is not the whole of Venus. It seems that there are already 2,6 km of mountains and mountain ranges that have already formed continents. Even at a surface temperature of 400 degrees Celsius, it is possible to have a temperature below 30 degrees Celsius, which is ideal for life to exist between the low temperatures in the highlands and the low temperatures. Unlike Mars, an environment with large temperature variations is the reason for its strong.
Sample 1. Equilateral oms// can maintain 30 degrees Celsius by combining high and low temperatures. Environmental change in degrees Celsius: (a+b+c)-(d+e+f)=(a+b+c=400 degrees) state-(d200+e100+f70=370 degrees) state = optimal temperature for living things 30 also state.
Venus can be lowered from 400 degrees Celsius to 30 degrees Celsius if the high temperature environment is lowered to low temperature sequentially in several stages due to the temperature difference between day and night on Venus.
Sample 1. Equilateral oms//
b0acfd 0000e0
000ac0 f00bde
0c0fab 000e0d
e00d0c 0b0fa0
f000e0 b0dac0
d0f000 cae0b0
0b000f 0ead0c
0deb00 ac000f
ced0ba 00f000
a0b00e 0dc0f0
0ace00 df000b
0f00d0 e0bc0a
Scientists have revived 100-million-year-old marine microbes
과학자들은 1 억년 된 해양 미생물을 되살 렸습니다

바다에서 가장 생명이없는 곳 중 하나에서 과학자들은 고대 유기체를 발견하고 소생시킵니다. 로비 버만 2020 년 7 월 31 일 형광 현미경으로 염색 된 세포 이미지 출처 : Morono, et al
-1 억년 전 죽은 것으로 보이는 미생물이 다시 살아납니다. 미생물은 태평양의 "포인트 니모"아래 깊숙이 묻혔습니다. 해저 아래에는 압도적 인 압력이 있지만이 미생물은 어쨌든 살아 남았습니다.
남태평양에는 육지에서 최대한 멀리 떨어진 곳이 있습니다. 이 " 접근 불가능한 해양 극 "은 지구 해양 표면의 10 %를 차지하는 남태평양 환류 아래에 있습니다. 너무 멀리 떨어져서 우주선이 임무가 끝날 때 정기적으로 바다로 안내됩니다. NASA 는 "태평양에 있으며 찾을 수있는 인류 문명에서 가장 먼 곳입니다."라고 말합니다. 그러나이 소위 " 포인트 니모 "가 다른 곳과 다르다는 또 다른 이유 가 있습니다. 그것은 바다의 사막 이며, 물이 늘어날 수있는 것처럼 표준 해양 생물이 거의 없습니다. 육지의 영양소는 도달 할 수 없으며 해류는 물을 나머지 바다와 격리시킵니다. 또한 과도한 자외선도 있습니다. 이 동안 이다 지역에 떠있는 일부 미생물 생명이, 일본과 미국 과학자의 팀은 아무것도 가능 지역의 황량한 해저에서 생활 할 수 있는지 알고 싶어. 그들이 발견하고 회수 한 것은 1 억년 동안 그곳에 갇혀있는 겉보기에는 생명이없는 미생물이었습니다. 작은 유기체는이 모든 시간이 지난 후에도 여전히 살아있는 것으로 나타났습니다. 필요한 것은 음식과 산소뿐이었습니다. “우리의 주된 질문은 영양이 제한된 환경에서 생명체가 존재할 수 있는지 아니면 이것이 생명이없는 지역인지 여부였습니다.” 라고 일본 해양-지구 과학 기술 청의 연구 책임자 인 미생물 학자 Yuki Morono 는 말합니다 . "그리고 우리는 미생물이 음식이 거의없는 상태에서 얼마나 오래 생존 할 수 있는지 알고 싶었습니다." 분명히 수억 년. 그것을 받아라, tardigrades . 학술지 Nature Communications 에 게재 된 연구 .
깊은 놀라움

태평양의 니모 포인트를 보여주는지도 이미지 출처 : martinova4 / 벡터 일러스트 / Shutterstock / Big Think 저 아래는 매우 친절한 환경이 아니며, 위의 모든 물의 무게가 그 아래에있는 모든 것을 세게 압박합니다. 이런 종류의 압력에 갇힌 유기체는 일반적으로 백만 년 정도면 죽고 화석화됩니다. 그럼에도 불구하고 어떤 이유로이 미생물들은 그 운명을 피했습니다. 공동 저자 인로드 아일랜드 대학의 지구 미생물학 자인 Steven D' Hondt 는 "우리는 많은 유기물이 묻혀있는 대륙 근처의 깊은 퇴적물에 생명체가 있다는 것을 알고있었습니다. 그러나 우리가 발견 한 것은 생명체가 해저에서 바닥에있는 암석 지하실까지 깊은 바다가 있습니다.

" 온보드 연구 Morono (왼쪽)와 D' Hondt (오른쪽)는 JODIES Resolution에 탑재 된 코어를 검사합니다. 이미지 출처 : IODP JRSO / 로드 아일랜드 대학교 미생물은 JOIDES Resolution 드릴 선박의 2010 년 Gyre 탐사 중에 해저에서 3.7 마일의 물을 통해 자랐습니다. 연구원들은 해저 아래 75 미터 (246 피트) 깊이의 원양 점토 퇴적물을 포함하여 다양한 사이트와 깊이에서 샘플을 추출했습니다. 선박의 퇴적물 코어를 조사한 연구진은 모든 깊이의 모든 샘플에서 적은 수의 산소 소모 미생물을 발견했습니다. 샘플을 코어에서 제거하여 거주자가 소생 될 수 있는지 확인했습니다. 그들은 주사기로 산소와 그들이 선택한 것으로 추정되는 음식, 탄소와 질소의 기질을 받았다. 그런 다음 샘플을 유리 바이알에 밀봉하고 배양했습니다.

미생물 성장 차트 탄소 (위)와 질소 (아래)를 먹인 후 미생물의 성장 이미지 출처 : Morono, et al
바이알은 21 일, 6 주 및 18 개월 후에 개봉되었습니다. 놀랍게도 최대 99 %의 미생물, 심지어 가장 깊은 (따라서 가장 오래된) 코어의 미생물까지도 부활했습니다. 일부는 자신이받은 탄소와 질소를 모두 소비하면서 그 수가 10,000 배 증가했습니다.
-과학자들은 그들이보고있는 것을 거의 믿을 수 없었습니다. 모로 노는 "처음에는 회의적 이었지만 1 억 150 만년 전에 퇴적 된 퇴적물에있는 미생물의 최대 99.1 %가 아직 살아 있고 먹을 준비가되어 있다는 것을 발견했습니다."라고 회상합니다. 끝없는 연구 기회 D-Hondt는 "그것은 세계 해양의 오래된 퇴적물에서 생명에 제한이 없음을 보여줍니다."라고 말합니다. "우리가 시추 한 가장 오래된 퇴적물에는 최소한의 음식으로도 여전히 살아있는 유기체가 있으며, 깨어나고 성장하고 번식 할 수 있습니다."
일부는 미생물이 1 억년 된 조상의 가장 최근의 후손 일 수 있다고 제안했지만 D' Hondt는 세포 분열을 지원할 영양분이나 에너지가 충분하지 않다고 말합니다. 즉, 어떤 형태의 방사선과 같이 간과 된 다른 형태의 에너지가없는 한 말입니다. "그들이 전혀 분열하지 않는다면 그들은 1 억년을 살고 있지만 그것은 미친 것 같다"고 그는 말한다 .
https://bigthink.com/surprising-science/100-million-microbes?rebelltitem=5#rebelltitem5
===메모 2106221743 나의 oms 스토리텔링
바다 사막의 해저 층, 1억년된 퇴적물에서 발견된 미생물이 먹이를 주자 부활했다. 1억년은 미생물의 잠재적인 생명의 회생 주기를 가진 것일 수도 있다.
적어도 미생물에 속하는 다른 종류이거나 더작은 생물체, 세포의 일부도 1억년을 살아갈 수 있는 것이 아닐까 싶다. 그것은 생명의 기본적인 주기인데 환경장애 때문에 생존이 단축된듯 하다.
이것이 사실이면 인간도 1억년을 살면서 은하계를 돌아 다닐 수도 있다는 함의이다. 특히 일부 주요장기 중에 뇌세포가 '1억년, 1조년을 생존할 수 있다'는 가정을 할 수 있다.
이 강력한 근거는 1억 등변 oms에서 1억된 미생물의 부활 주기를 설명될 수 있을듯 하다. 허허.
Sample 1. 등변oms//미생물이나 세포들의 1억년 생명주기
b0acfd 0000e0
000ac0 f00bde
0c0fab 000e0d
e00d0c 0b0fa0
f000e0 b0dac0
d0f000 cae0b0
0b000f 0ead0c
0deb00 ac000f
ced0ba 00f000
a0b00e 0dc0f0
0ace00 df000b
0f00d0 e0bc0a

-Scientists could hardly believe what they were seeing. "I was skeptical at first," Morono recalls, "but we found that up to 99.1 percent of the microbes in sediments deposited 115 million years ago were still alive and ready to eat." Endless Research Opportunities "It shows no limits to life in old sediments in the world's oceans," says D-Hondt. "In the oldest sediments we've drilled, there are still living organisms with minimal food, and they can wake up, grow and reproduce."
=== memo 2106221743 my oms storytelling
Microorganisms found in 100-million-year-old sediments in the seabed of sea deserts revived when fed. 100 million years could be a potential life cycle of microorganisms.
At least, other types of microorganisms, or smaller organisms, and parts of cells can live for 100 million years. It is a basic cycle of life, but it seems that the survival is shortened due to environmental disorders.
If this is true, it would imply that humans could live 100 million years and travel around the galaxy. In particular, among some major organs, it can be assumed that brain cells can survive for 100 million years or 1 trillion years.
This strong evidence could explain the life cycle of 100 million microbes at 100 million equilateral oms. haha.
Sample 1. Isosceles oms // 100 million year life cycle of microorganisms or cells
b0acfd 0000e0
000ac0 f00bde
0c0fab 000e0d
e00d0c 0b0fa0
f000e0 b0dac0
d0f000 cae0b0
0b000f 0ead0c
0deb00 ac000f
ced0ba 00f000
a0b00e 0dc0f0
0ace00 df000b
0f00d0 e0bc0a
.Math Duo Maps the Infinite Terrain of Minimal Surfaces Math
Duo는 최소 표면의 무한 지형을 매핑합니다

한 쌍의 수학자는 비누 필름과 같은 최소 표면이 다양한 형태로 풍부하게 나타나는 것을 보여주기 위해 모호한 30 년 된 수학적 이론을 구축했습니다. 3 나중에 읽기 Ted Kinsman / 과학 출처

에리카 클라 라이히 기고 특파원 2019 년 3 월 12 일
앨리스와 밥이 불의 벽을 만나다-Quanta의 과학 분야에서 가장 큰 아이디어 – 지금 구입 가능!
2011 년 마지막 달에 Brian White 는 때때로 스탠포드 대학 사무실 문을 두드리는 소리를 듣곤했습니다. 밖에서 기다리는 두 명의 젊은 수학자 Fernando Codá Marques 와 André Neves 는 항상 똑같은 대략적인 질문을했습니다.
White는 30 년 전에 작성된 모호한 수백 페이지의 박사 학위 논문의 일부 혼란스러운 부분을 이해할 수 있도록 몇 분 동안 도움을 주 었나요 ? ? Jon Pitts 의 논문 은 다양한 모양 내에서 최소 표면 (비누 필름 및 거품과 유사한 구조)을 구성하기위한 강력한 기계를 제시했습니다.
최소한의 표면을 구성 할 수있을 때 주변 공간의 기하학을 연구 할 수있는 렌즈를 제공하고 블랙홀 연구에서 생체 분자 설계에 이르기까지 다양한 과학적 환경에서 나타납니다. 그러나 수년 동안 Pitts의 논문은 아마도 믿을 수 없을 정도로 읽기 힘들었 기 때문에 시야에서 사라졌습니다.
Marques와 Neves는 아직 개발되지 않은 잠재력으로 가득 차 있다고 확신했습니다. 현재 시카고 대학의 교수 인 Neves는“이론이 완전히 과소 평가되었고 전혀 눈에 띄지 않았다는 것이 우리에게 분명했습니다. White는 Pitts의 작업에 왜 관심이 있는지 묻지 않았지만, 두 사람은 방문 할 때마다 "그냥 학문적 관심"이라고 주장 할 준비를했습니다. 그러나 그들은 특정한 목표를 염두에 두었습니다.
Willmore 추측의 증거, 어떤 의미에서는 최상의 도넛 모양을 찾는 것에 대한 50 년 된 질문입니다 (이에 대해서는 나중에 자세히 설명합니다). 3 개월 동안 Pitts의 논문에서 아이디어와 씨름 한 끝에 Marques와 Neves 는이 목표를 달성 하여 수많은 상과 찬사를 받았습니다. 그러나 지난 몇 년 동안 그들은 Pitts의 아이디어를 훨씬 더 발전시킬 수있었습니다. Pitts와 그의 고문 인 Frederick Almgren은 모든 저 차원 형상에 최소한 하나의 최소 표면이 포함되도록 보장하는 방법을 찾았습니다.
이제 Marques와 Neves는 주변에서 생겨난 젊은 수학자 간부와 함께 Almgren과 Pitts의 아이디어를 바탕으로 일반적으로 이러한 모양이 실제로 수많은 최소 표면을 포함해야 함을 보여줍니다. 모양의 구석 구석을 붐비고 밀집합니다. 오스틴에있는 텍사스 대학의 저명한 기하학자인 Karen Uhlenbeck 은 이메일에서 “이것은 큰 돌파구 입니다. 거의 15 년 전에 Neves의 박사 고문이었던 Irvine 소재 캘리포니아 대학의 Richard Schoen 은 "단지 [최소한의 표면]을 만드는 것만으로도 엄청난 노력을 기울였습니다."라고 말했습니다 . "이것들이 너무나 많이 존재한다는 것은 정말 놀라운 사실입니다." Almgren과 Pitts 이론의 이러한 르네상스로 인해 지난 1 ~ 2 년 동안 활동이 폭발적으로 증가했습니다. "결과가 너무 두껍고 빠르게 나오고있어 따라 가기가 조금 어렵습니다."라고 White는 말했습니다.
“저에게는 매우 흥미롭고 훌륭합니다.” 산맥 차트 작성 구부러진 와이어 프레임을 비누 용액에 담 그거나 비눗 방울을 불어 넣으면 액체가 가능한 최소한의 영역으로 표면을 빠르게 형성합니다. 이러한 "최소한"표면의 기하학적 구조는 수백 년 동안 수학자를 점유 해 왔으며, 지붕 및 기타 구조의 디자인에 영감을주는 건축에서부터 약물 전달을위한 미세 입자 생성에 이르기까지 주제에서 발생합니다. 예를 들어, 5 년 전 과학자 팀이 약물이나 호르몬을 보유 할 수있는 다공성 분자 를 제작 했을 때 분자 중 일부가 자이 로이드와 같은 구조를 취하고 있다는 사실을 발견했습니다. 약간의 비누 필름. 기술적으로 수학자들은 와이어 프레임 비누 필름을 비누 방울이 아닌 최소 표면으로 만 계산합니다.
공기 분자가없는 추상 공간에서는 비누 방울이 단일 지점으로 붕괴되기 때문입니다. 그러나 와이어에있는 비누 필름조차도 수학자들에게 완벽하게 만족스럽지 않습니다. 내부는 멋진 표면을 형성하지만 와이어 프레임은 갑작스러운 구두점 역할을합니다. 이러한 표면을 고려할 때 와이어 경계를 넘어 확장 되어도 작은 패치마다 비누 필름처럼 보일 수 있는지 궁금해하는 것은 당연합니다. 때로는 이것이 가능하며 표면은 무한대로 확장됩니다. 다른 때는 표면이 돌아와 어색하게 교차하거나 다른 어려움에 부딪 힐 것입니다.

3D 삽화 : 자이 로이드 자이 로이드는 약물 전달을위한 미세 입자 설계에서 잘린 최소 표면 유형입니다.
평범한 공간에서는 이것이 유일한 가능성입니다. 하지만 수학자와 과학자들은 종종 우리가 생각하던 무한한 3 차원 공간이 아닌 다른 유형의 세계를 고려할 기회가 있습니다. 구 또는 도넛 표면의 3 차원 유사체처럼 구부러 지거나 크기가 유한 한 세계 . 이러한 모양 내에서 새롭고 흥미로운 가능성이 나타납니다.
최소한의 표면이 다시 구부러져 와이어 지원이 필요없는 완전하고 유한 한 모양으로 닫힙니다. 상대성 이론에서 이러한 유한 한 최소 표면은 블랙홀의 사건 지평선으로 나타납니다. 그리고 그것들이 어떤 모양 안에서 발견 될 때, 그들은 수학자들이 다양한 방식으로 그 기하학을 이해하도록 도와줍니다. 그들은 모양 (또는“다양체”)을 잠재적으로 더 단순한 조각으로 자르기위한 템플릿을 제공하고, 그 안의 양의 곡률 영역을 가리 킵니다.
다기관 — 바깥쪽으로 퍼지는 대신구나 블랙홀처럼 안쪽으로 구부러지는 영역. Schoen은“양의 곡률의 다양한 종류에 대해 잘 모릅니다. 그러나 모양 안에 유한 한 최소 표면이 존재한다는 것을 증명하는 것은 종종 쉬운 일이 아닙니다. 이유를 알아 보려면이 문제의 2 차원 버전을 고려하십시오. 최소 표면을 찾는 문제는 모든 차원에서 의미가 있습니다. 수학자들은 단순히 "표면"을 그것이 사는 공간보다 한 차원 낮은 모양으로 간주합니다. 따라서 2 차원 세계에서 최소 표면은 "측 지적"입니다. 가까운 지점 사이의 최단 경로로 구성된 곡선. 일부 2 차원 모양의 경우 유한 루프로 가까운 측지선을 쉽게 찾을 수 있습니다. 예를 들어 도넛 표면을 예로 들어 보겠습니다.
꼭 둥글고 대칭적인 도넛 일 필요는 없지만 요철이있는 도넛 표면입니다. 도넛 주위에 고무 밴드를 감아 중앙 구멍을 통과하면 단단히 잡아 당긴 다음 표면을 따라 가능한 모든 위치로 미끄러지는 것을 상상할 수 있습니다. 이러한 구성 중 하나는 가장 짧아야하며, 그렇지 않으면 더 짧게 할 수 있기 때문에 측지선이어야합니다. FIGURE: drawing of a doughnut 그러나 우리의 모양이 도넛 대신 구면이 접근 방식은 실패합니다. 완벽하게 둥근 구에서는 측지선을 쉽게 식별 할 수 있습니다. 그들은 적도와 다른 "큰 원"입니다. 그러나 지구 표면과 같은 울퉁불퉁 한 구에서는 측지선이 어디로 가는지 또는 그 중 어떤 것이 유한 루프로 닫히는 지 명확하지 않습니다. 우리가 도넛으로했던 것처럼 지구를 고무줄로 감싸는 것을 상상할 수 있습니다. 그러나 길이를 줄이려고 밀어 주면 도넛과 달리 구에는 고무줄이 끼일 수있는 구멍이 없기 때문에 단일 지점으로 축소됩니다. 그러나이 러버 밴드 실패는 실제로 성공의 씨앗을 가지고 있습니다.
둥근 구체에서 적도에 고무 밴드가있는 것을 상상한다면 그것을 이동시키는 한 가지 방법, 즉 흔들림을 도입하는 것입니다. 이동하는 또 다른 방법 (새 위도까지 똑바로 위 또는 아래로 슬라이드)하면 길이가 더 짧아집니다. 따라서 적도는 한 시점에서 가장 짧은 곡선이고 다른 시점에서 가장 긴 곡선입니다. 이는 적도를 한 방향 (고개 위의 경로)에서 가장 높은 지점이고 다른 방향에서 가장 낮은 지점 (주변 봉우리까지의 경로) 인 산길 꼭대기의 안장 지점과 유사하게 만듭니다. 이것은 모호한 비유가 아닙니다. 일반적으로 최소한의 표면은 실제로 안장 지점이지만, 그들의 산맥은 우리의 평범한 것보다 시각화하기 훨씬 더 어려운 세계에 살고 있습니다.
Lucy Reading-Ikkanda / Quanta 잡지
모양 내에서 최소 표면을 찾을 때 모양에있는 모든 가능한 유한 표면으로 구성된 새로운 세계를 고려할 수 있습니다.이 세계를 "표면 공간"이라고합시다. 표면 공간의 각 점은 원래 모양의 전체 표면에 해당합니다. 다음으로, 우리는 각 표면의 면적을 표면 공간에서 해당 지점의 고도를 결정하는 것으로 생각하여 새로운 세계가 자연스러운 지형을 갖도록 할 수 있습니다. 원래 모양에서 최소한의 표면을 찾는 것은 표면 공간에서 안장 지점을 찾는 것으로 해석됩니다. 1917 년에 George Birkhoff 는이 접근 방식을 사용하여 울퉁불퉁하거나 둥근 구에는 적어도 하나의 폐쇄 측지선이 있어야 함 을 보여주었습니다 .
그리고 약 60 년 후, Birkhoff의 아이디어를 뚜르 드 포스로 확장하여 Almgren과 Pitts는 3 ~ 7 차원의 모든 유한 형상에 대한 표면 공간의 지형을 매핑 한 다음 그 지형을 사용하여 이러한 형상이 항상 하나 이상의 닫힌 최소 표면. 이“minmax”이론에 대한 Pitts의 1981 년 논문 ( 안장 지점이 최소값과 최대 값이기 때문에 명명 됨)은“절대적으로 탁월합니다”라고 Neves는 말했습니다. 그러나 그것은 또한 매우 어려웠다. 이론의 뉘앙스를 이해하는 사람은 거의 없었고,이를 연구하는 일부 수학자들은 완전히 검증되지 않은 주장을했다. "매우 흥미롭고 중요했다는 데는 의심의 여지가 없었습니다."라고 그는 말했습니다. 그러나“이게 얼마나 철저한지는 분명하지 않았습니다.” minmax 이론에 대한 작업은 점차 줄어 들었습니다.
Neves는“[Pitts의] 작업은 수학적 커뮤니티에서 아마 30 년 동안 잊혀졌습니다. Neves와 Marques는 2006 년 Princeton University의 수학 건물 인 Fine Hall의 엘리베이터에서 만났을 때까지 부활하지 않았습니다. 산길 너머 그 당시 Marques는 연설을하기 위해 Princeton을 방문하고있었습니다. Neves는 최근 그곳에서 박사후 과정을 시작했습니다. 두 명의 포르투갈어 원어민 (Marques는 브라질 출신, Neves는 포르투갈 출신)으로 쉽게 대화에 빠져 들었습니다. 지금 프린스턴의 교수 인 Marques는 "처음으로 그와 이야기를 나눴지만 그는 마치 우리가 10 년 동안 친구 인 것처럼 이야기했습니다. 그리고 그들은 함께 수학을 논의하는 것이 자연스럽게 이루어 졌다는 것을 발견했습니다. 두 사람은 서로 다른 스타일을 가졌습니다.
Marques는 참을성이 있고 Neves는 더 강렬했습니다. 그러나 이것은 플러스였다. Marques는 "당신을 보완 해주는 사람을 찾는 것은 매우 드뭅니다."라고 말했습니다. 두 사람 모두 자신의 이빨을 가라 앉힐 수있는 수학적 도전을 찾고 싶어했습니다. 몇 년 동안 두 사람은 길을 건너 갈 때마다 아이디어를 던져 "어떤 것이 달라지는 지"확인했습니다. "우리는 수백만 개의 아이디어를 갖게되었고 결국 하나의 아이디어가 걸러 져서 형성되는 것이됩니다." 결국 여과 된 큰 도전은 Willmore 추측이라는 유명한 문제였습니다. 이것은 대략적으로 말하면 둥근 구와 모양이 얼마나 다른지 측정하는 Willmore 에너지라는 양을 최소화하는 도넛 모양을 요구합니다. 윌 모어는 1965 년에 가장 둥근 도넛이 특히 클리포드 토러스라고 불리는 대칭 모양이라고 추측 했지만, 많은 시도에도 불구하고 아무도 이것을 증명할 수 없었습니다.
Ana Menezes (Marques); André Neves의 의례 Marques와 Neves는 유망한 접근 방식을 개발했지만 제대로 작동하려면 최종 요소 인 minmax 이론이 필요했습니다. 그들은 이론을 습득하고 논문을 작성하는 데 Pitts의 책을 열 때까지 2-3 주가 소요될 것이라고 생각했습니다. "우리는 충격을 받았습니다.이게 뭐죠?" 네 베스는 말했다.
"이 책은 엄청나게 마른 책입니다." 단일 정리는 페이지를 위해 계속되었습니다. 그리고 그것은 증명은 말할 것도없이 정리를 진술하는 것입니다. 주 정리를 찾는 것도 어려웠습니다. "나는 Fernando가 내 사무실에 와서 '정리의 진술을 찾았습니다!'라고 말한 것을 기억합니다."Neves가 말했습니다. 그들이 막혔을 때, 그들은 포커 페이스를 쓰고 Pitts의 작업을 많이 이해 한 유일한 사람 중 한 명인 White에게 도움을 요청했습니다. College Station에있는 Texas A & M University의 교수 인 그는 수십 년 전에 minmax 이론에 대한 논문 작성을 중단했습니다.) Neves는 이렇게 회상합니다.
"우리는 믿을 수 없을만큼 의욕이 넘 쳤기 때문에 추진할 수있었습니다." "그러나 그것은 희미한 마음을위한 것이 아닙니다." Marques와 Neves가 Willmore 추측에 대한 증명을 마쳤을 때, 그들은 아마도 다른 수학자보다 최소값 이론을 더 잘 이해했습니다. 그들은 그 잠재력이 Willmore 추측보다 훨씬 더 확장되었다고 확신했습니다. Neves는“우리는 믿을 수 없을 정도로 강력한이 이론을 가지고 있다는 것을 알고있었습니다. “방법을 사용할 때마다 한동안 열려있는 결과를 증명할 수 있으며, 그 결과에 무언가가 있음을 알려줍니다.
계속 밀어 붙이는 것이 가치가 있다는 것을 알려줍니다.” Almgren과 Pitts의 minmax 기계는 단일 안장 지점뿐만 아니라 무한 목록을 생성합니다. 이론적으로 이들은 원래 모양의 최소 표면 목록에 해당해야합니다. 그러나 Almgren과 Pitts는 이러한 방식으로 생성 된 최소한의 표면이 모두 다른 표면이라는 것을 보여줄 수 없었습니다. 그래서 그들이 결론을 내릴 수있는 가장 큰 것은 원래 모양이 최소한 하나의 최소한의 표면을 가지고 있다는 것입니다. 그 후, "대상은 거의 멈췄습니다"라고 Neves는 말했습니다.
"이것은 30 년 넘게 최고의 결과였습니다." 몇 가지 새로운 재료가 필요했고 Marques와 Neves가 하나를 찾았습니다. 그들이 2016 년에 보여준 무한한 최소 표면 목록은 드럼의 주파수와 매우 유사하게 특정 방식으로 작동합니다. 수학자 헤르만 웨일 (Hermann Weyl)은 1911 년 드럼의 기본 주파수가 놀라운 특성을 가지고 있음을 보여주었습니다. 대략적으로 말하면 고주파는 드럼의 모양이 아니라 볼륨에 의존합니다. Marques와 Neves 는 Massachusetts Institute of Technology의 Yevgeny Liokumovich 와 함께 minmax 표면이 드럼 주파수와 유사한 수학적 법칙을 충족 함을 보여주었습니다 .
특히 표면의 영역 (특히 목록에서 더 먼 영역)은 대략적으로 그들이 살고있는 공간의 부피에 의해 결정되지만 모양은 아닙니다. 수십 년 전의 추측을 해결 한이 결과는 Marques와 Neves가 2017 년에 -이번에 는 도쿄 대학의 Kei Irie 와 공동으로 -대부분의 모양에 대해 minmax 목록에 무한히 많은 다른 최소 표면이 포함되어 있음 을 보여줄 수있었습니다 . 더욱이, 그들은 이러한 표면이“밀집”하다는 것을 보여주었습니다. 그들은 주변 공간의 모든 지점 근처에서 나타납니다. 이 공제이면의 직관은 공간의 볼륨이 최소 표면의 영역을 결정하기 위해 이러한 표면이 어떻게 든 전체 볼륨을 "보아야"한다는 것입니다. 이것은 "이 사람들이 다기관의 모든 곳에 있음을 시사한다"고 Marques는 말했다. 그리고 몇 달 후 Marques의 대학원생 Antoine Song 과 공동 으로이 쌍은 최소 최대 표면 목록을 따라 가면 이러한 표면이 공간을 고르게 채우는 경향이 있음을 보여주었습니다 . 수학자들은 "등분 포"라고합니다. 화이트는“그들이 균등하게 분포되어 있다는 결과를 듣고 놀랐습니다. "사람들이 내 생애에서 증명할 수있는 것 이상으로 보였습니다." 지난 몇 년 동안 다른 수학자들이 행동에 뛰어 들었습니다. 예를 들어, 1 월에 산타 바바라에있는 캘리포니아 대학의 Xin Zhou 는 Marques와 Neves의 이전 작업 을 기반 으로 대부분의 모양에 대해 Almgren과 Pitts의 목록에있는 모든 최소 표면이 다르다는 것을 증명 했습니다. 폐쇄. “80 년대에 Almgren-Pitts 제품이 출시 된 이후로 열려있는이 제품의 멋진 패키지를 만듭니다.”라고 White가 말했습니다.
이 결과 군은 3 ~ 7 개 사이의 거의 모든 형태의 차원을 다룹니다. 거의 모든 형태를 다루고 있습니다. 그러나 가장 둥근 형태를 제외하고는 반 직관적으로 충분합니다. 그러나 지난 6 월 송은 가장 둥근 모양을 포함하여 이러한 차원의 모든 단일 모양이 무한히 많은 닫힌 최소 표면을 가지고 있음을 증명 하여 또 다른 수십 년 된 추측을 해결했습니다. 밀도와 균등 분포가이 더 넓은 설정으로 이어질지, 최소값 이론의 어느 부분이 콤팩트하지 않은 매니 폴드와 차원이 8 이상인 매니 폴드 ( 새 논문이 이미 약간의 진전이있었습니다). 수학자들은 이러한 질문들 중 많은 부분이 늦어지기보다는 더 빨리 대답 될 것이라고 예측합니다. Neves는“상황이 매우 빠르게 진행되고 있습니다. "이제 매주 [과학적 사전 인쇄 사이트] arxiv를 봅니다. 누군가 방금 다른 문제를 해결했습니다." 관련 : 추상 표면의 끈질긴 탐험가 복잡한 시스템에 대한 단서를 제공하는 3 차원 프랙탈 과학자들은 편평함으로부터 곡선을 만들어 낸다 한 관점에서이 작업은 거의 40 년 동안 미완성으로 얽혀있는 이야기의 끝 (또는 끝에 가까움)을 표시합니다. 그러나 그것은 또한 새로운 시작입니다. 수학자들은 최소한의 표면에 대한 이러한 새로운 통찰이 그들이 사는 공간에 대해 우리에게 말해 줄 수있는 것을 이해하기 시작했습니다. Schoen은 "다른 극적인 응용 프로그램이 나올 것이라고 생각하지만 현재로서는 정확히 무엇을 말할 수 없습니다."라고 말했습니다. "기하학의 주요 방향이 될 것입니다."
편집자 주 : André Neves는 2018 년에 Simons Investigator로 지명되었습니다. Simons Foundation은 또한이 편집 독립 잡지에 자금을 지원합니다 .
평범한 공간에서는 이것이 유일한 가능성입니다. 하지만 수학자와 과학자들은 종종 우리가 생각하던 무한한 3 차원 공간이 아닌 다른 유형의 세계를 고려할 기회가 있습니다. 구 또는 도넛 표면의 3 차원 유사체처럼 구부러 지거나 크기가 유한 한 세계 . 이러한 모양 내에서 새롭고 흥미로운 가능성이 나타납니다.
최소한의 표면이 다시 구부러져 와이어 지원이 필요없는 완전하고 유한 한 모양으로 닫힙니다. 상대성 이론에서 이러한 유한 한 최소 표면은 블랙홀의 사건 지평선으로 나타납니다. 그리고 그것들이 어떤 모양 안에서 발견 될 때, 그들은 수학자들이 다양한 방식으로 그 기하학을 이해하도록 도와줍니다. 그들은 모양 (또는“다양체”)을 잠재적으로 더 단순한 조각으로 자르기위한 템플릿을 제공하고, 그 안의 양의 곡률 영역을 가리 킵니다.
다기관 — 바깥쪽으로 퍼지는 대신구나 블랙홀처럼 안쪽으로 구부러지는 영역. Schoen은“양의 곡률의 다양한 종류에 대해 잘 모릅니다. 그러나 모양 안에 유한 한 최소 표면이 존재한다는 것을 증명하는 것은 종종 쉬운 일이 아닙니다. 이유를 알아 보려면이 문제의 2 차원 버전을 고려하십시오. 최소 표면을 찾는 문제는 모든 차원에서 의미가 있습니다. 수학자들은 단순히 "표면"을 그것이 사는 공간보다 한 차원 낮은 모양으로 간주합니다. 따라서 2 차원 세계에서 최소 표면은 "측 지적"입니다. 가까운 지점 사이의 최단 경로로 구성된 곡선. 일부 2 차원 모양의 경우 유한 루프로 가까운 측지선을 쉽게 찾을 수 있습니다. 예를 들어 도넛 표면을 예로 들어 보겠습니다.
꼭 둥글고 대칭적인 도넛 일 필요는 없지만 요철이있는 도넛 표면입니다. 도넛 주위에 고무 밴드를 감아 중앙 구멍을 통과하면 단단히 잡아 당긴 다음 표면을 따라 가능한 모든 위치로 미끄러지는 것을 상상할 수 있습니다. 이러한 구성 중 하나는 가장 짧아야하며, 그렇지 않으면 더 짧게 할 수 있기 때문에 측지선이어야합니다. FIGURE: drawing of a doughnut 그러나 우리의 모양이 도넛 대신 구면이 접근 방식은 실패합니다. 완벽하게 둥근 구에서는 측지선을 쉽게 식별 할 수 있습니다.

그들은 적도와 다른 "큰 원"입니다. 그러나 지구 표면과 같은 울퉁불퉁 한 구에서는 측지선이 어디로 가는지 또는 그 중 어떤 것이 유한 루프로 닫히는 지 명확하지 않습니다. 우리가 도넛으로했던 것처럼 지구를 고무줄로 감싸는 것을 상상할 수 있습니다. 그러나 길이를 줄이려고 밀어 주면 도넛과 달리 구에는 고무줄이 끼일 수있는 구멍이 없기 때문에 단일 지점으로 축소됩니다. 그러나이 러버 밴드 실패는 실제로 성공의 씨앗을 가지고 있습니다.
둥근 구체에서 적도에 고무 밴드가있는 것을 상상한다면 그것을 이동시키는 한 가지 방법, 즉 흔들림을 도입하는 것입니다. 이동하는 또 다른 방법 (새 위도까지 똑바로 위 또는 아래로 슬라이드)하면 길이가 더 짧아집니다. 따라서 적도는 한 시점에서 가장 짧은 곡선이고 다른 시점에서 가장 긴 곡선입니다. 이는 적도를 한 방향 (고개 위의 경로)에서 가장 높은 지점이고 다른 방향에서 가장 낮은 지점 (주변 봉우리까지의 경로) 인 산길 꼭대기의 안장 지점과 유사하게 만듭니다. 이것은 모호한 비유가 아닙니다. 일반적으로 최소한의 표면은 실제로 안장 지점이지만, 그들의 산맥은 우리의 평범한 것보다 시각화하기 훨씬 더 어려운 세계에 살고 있습니다.

Lucy Reading-Ikkanda / Quanta 잡지
모양 내에서 최소 표면을 찾을 때 모양에있는 모든 가능한 유한 표면으로 구성된 새로운 세계를 고려할 수 있습니다.이 세계를 "표면 공간"이라고합시다. 표면 공간의 각 점은 원래 모양의 전체 표면에 해당합니다. 다음으로, 우리는 각 표면의 면적을 표면 공간에서 해당 지점의 고도를 결정하는 것으로 생각하여 새로운 세계가 자연스러운 지형을 갖도록 할 수 있습니다. 원래 모양에서 최소한의 표면을 찾는 것은 표면 공간에서 안장 지점을 찾는 것으로 해석됩니다. 1917 년에 George Birkhoff 는이 접근 방식을 사용하여 울퉁불퉁하거나 둥근 구에는 적어도 하나의 폐쇄 측지선이 있어야 함 을 보여주었습니다 .
그리고 약 60 년 후, Birkhoff의 아이디어를 뚜르 드 포스로 확장하여 Almgren과 Pitts는 3 ~ 7 차원의 모든 유한 형상에 대한 표면 공간의 지형을 매핑 한 다음 그 지형을 사용하여 이러한 형상이 항상 하나 이상의 닫힌 최소 표면. 이“minmax”이론에 대한 Pitts의 1981 년 논문 ( 안장 지점이 최소값과 최대 값이기 때문에 명명 됨)은“절대적으로 탁월합니다”라고 Neves는 말했습니다. 그러나 그것은 또한 매우 어려웠다. 이론의 뉘앙스를 이해하는 사람은 거의 없었고,이를 연구하는 일부 수학자들은 완전히 검증되지 않은 주장을했다. "매우 흥미롭고 중요했다는 데는 의심의 여지가 없었습니다."라고 그는 말했습니다. 그러나“이게 얼마나 철저한지는 분명하지 않았습니다.” minmax 이론에 대한 작업은 점차 줄어 들었습니다.
Neves는“[Pitts의] 작업은 수학적 커뮤니티에서 아마 30 년 동안 잊혀졌습니다. Neves와 Marques는 2006 년 Princeton University의 수학 건물 인 Fine Hall의 엘리베이터에서 만났을 때까지 부활하지 않았습니다. 산길 너머 그 당시 Marques는 연설을하기 위해 Princeton을 방문하고있었습니다. Neves는 최근 그곳에서 박사후 과정을 시작했습니다. 두 명의 포르투갈어 원어민 (Marques는 브라질 출신, Neves는 포르투갈 출신)으로 쉽게 대화에 빠져 들었습니다. 지금 프린스턴의 교수 인 Marques는 "처음으로 그와 이야기를 나눴지만 그는 마치 우리가 10 년 동안 친구 인 것처럼 이야기했습니다. 그리고 그들은 함께 수학을 논의하는 것이 자연스럽게 이루어 졌다는 것을 발견했습니다. 두 사람은 서로 다른 스타일을 가졌습니다.
Marques는 참을성이 있고 Neves는 더 강렬했습니다. 그러나 이것은 플러스였다. Marques는 "당신을 보완 해주는 사람을 찾는 것은 매우 드뭅니다."라고 말했습니다. 두 사람 모두 자신의 이빨을 가라 앉힐 수있는 수학적 도전을 찾고 싶어했습니다. 몇 년 동안 두 사람은 길을 건너 갈 때마다 아이디어를 던져 "어떤 것이 달라지는 지"확인했습니다. "우리는 수백만 개의 아이디어를 갖게되었고 결국 하나의 아이디어가 걸러 져서 형성되는 것이됩니다." 결국 여과 된 큰 도전은 Willmore 추측이라는 유명한 문제였습니다. 이것은 대략적으로 말하면 둥근 구와 모양이 얼마나 다른지 측정하는 Willmore 에너지라는 양을 최소화하는 도넛 모양을 요구합니다. 윌 모어는 1965 년에 가장 둥근 도넛이 특히 클리포드 토러스라고 불리는 대칭 모양이라고 추측 했지만, 많은 시도에도 불구하고 아무도 이것을 증명할 수 없었습니다.

초상화 : Fernando Codá Marques 초상화 : André Neves 2013 년 윌 모어 추측을 입증 한 후 Fernando Codá Marques (왼쪽)와 André Neves는 계속해서 최소 표면 연구에서 획기적인 결과를 달성했습니다.
Ana Menezes (Marques); André Neves의 의례 Marques와 Neves는 유망한 접근 방식을 개발했지만 제대로 작동하려면 최종 요소 인 minmax 이론이 필요했습니다. 그들은 이론을 습득하고 논문을 작성하는 데 Pitts의 책을 열 때까지 2-3 주가 소요될 것이라고 생각했습니다. "우리는 충격을 받았습니다.이게 뭐죠?" 네 베스는 말했다.
"이 책은 엄청나게 마른 책입니다." 단일 정리는 페이지를 위해 계속되었습니다. 그리고 그것은 증명은 말할 것도없이 정리를 진술하는 것입니다. 주 정리를 찾는 것도 어려웠습니다. "나는 Fernando가 내 사무실에 와서 '정리의 진술을 찾았습니다!'라고 말한 것을 기억합니다."Neves가 말했습니다. 그들이 막혔을 때, 그들은 포커 페이스를 쓰고 Pitts의 작업을 많이 이해 한 유일한 사람 중 한 명인 White에게 도움을 요청했습니다. College Station에있는 Texas A & M University의 교수 인 그는 수십 년 전에 minmax 이론에 대한 논문 작성을 중단했습니다.) Neves는 이렇게 회상합니다.
"우리는 믿을 수 없을만큼 의욕이 넘 쳤기 때문에 추진할 수있었습니다." "그러나 그것은 희미한 마음을위한 것이 아닙니다." Marques와 Neves가 Willmore 추측에 대한 증명을 마쳤을 때, 그들은 아마도 다른 수학자보다 최소값 이론을 더 잘 이해했습니다. 그들은 그 잠재력이 Willmore 추측보다 훨씬 더 확장되었다고 확신했습니다. Neves는“우리는 믿을 수 없을 정도로 강력한이 이론을 가지고 있다는 것을 알고있었습니다. “방법을 사용할 때마다 한동안 열려있는 결과를 증명할 수 있으며, 그 결과에 무언가가 있음을 알려줍니다.
계속 밀어 붙이는 것이 가치가 있다는 것을 알려줍니다.” Almgren과 Pitts의 minmax 기계는 단일 안장 지점뿐만 아니라 무한 목록을 생성합니다. 이론적으로 이들은 원래 모양의 최소 표면 목록에 해당해야합니다. 그러나 Almgren과 Pitts는 이러한 방식으로 생성 된 최소한의 표면이 모두 다른 표면이라는 것을 보여줄 수 없었습니다. 그래서 그들이 결론을 내릴 수있는 가장 큰 것은 원래 모양이 최소한 하나의 최소한의 표면을 가지고 있다는 것입니다. 그 후, "대상은 거의 멈췄습니다"라고 Neves는 말했습니다.
"이것은 30 년 넘게 최고의 결과였습니다." 몇 가지 새로운 재료가 필요했고 Marques와 Neves가 하나를 찾았습니다. 그들이 2016 년에 보여준 무한한 최소 표면 목록은 드럼의 주파수와 매우 유사하게 특정 방식으로 작동합니다. 수학자 헤르만 웨일 (Hermann Weyl)은 1911 년 드럼의 기본 주파수가 놀라운 특성을 가지고 있음을 보여주었습니다. 대략적으로 말하면 고주파는 드럼의 모양이 아니라 볼륨에 의존합니다. Marques와 Neves 는 Massachusetts Institute of Technology의 Yevgeny Liokumovich 와 함께 minmax 표면이 드럼 주파수와 유사한 수학적 법칙을 충족 함을 보여주었습니다 .
특히 표면의 영역 (특히 목록에서 더 먼 영역)은 대략적으로 그들이 살고있는 공간의 부피에 의해 결정되지만 모양은 아닙니다. 수십 년 전의 추측을 해결 한이 결과는 Marques와 Neves가 2017 년에 -이번에 는 도쿄 대학의 Kei Irie 와 공동으로 -대부분의 모양에 대해 minmax 목록에 무한히 많은 다른 최소 표면이 포함되어 있음 을 보여줄 수있었습니다 . 더욱이, 그들은 이러한 표면이“밀집”하다는 것을 보여주었습니다. 그들은 주변 공간의 모든 지점 근처에서 나타납니다. 이 공제이면의 직관은 공간의 볼륨이 최소 표면의 영역을 결정하기 위해 이러한 표면이 어떻게 든 전체 볼륨을 "보아야"한다는 것입니다. 이것은 "이 사람들이 다기관의 모든 곳에 있음을 시사한다"고 Marques는 말했다. 그리고 몇 달 후 Marques의 대학원생 Antoine Song 과 공동 으로이 쌍은 최소 최대 표면 목록을 따라 가면 이러한 표면이 공간을 고르게 채우는 경향이 있음을 보여주었습니다 . 수학자들은 "등분 포"라고합니다. 화이트는“그들이 균등하게 분포되어 있다는 결과를 듣고 놀랐습니다. "사람들이 내 생애에서 증명할 수있는 것 이상으로 보였습니다." 지난 몇 년 동안 다른 수학자들이 행동에 뛰어 들었습니다. 예를 들어, 1 월에 산타 바바라에있는 캘리포니아 대학의 Xin Zhou 는 Marques와 Neves의 이전 작업 을 기반 으로 대부분의 모양에 대해 Almgren과 Pitts의 목록에있는 모든 최소 표면이 다르다는 것을 증명 했습니다. 폐쇄. “80 년대에 Almgren-Pitts 제품이 출시 된 이후로 열려있는이 제품의 멋진 패키지를 만듭니다.”라고 White가 말했습니다.
이 결과 군은 3 ~ 7 개 사이의 거의 모든 형태의 차원을 다룹니다. 거의 모든 형태를 다루고 있습니다. 그러나 가장 둥근 형태를 제외하고는 반 직관적으로 충분합니다. 그러나 지난 6 월 송은 가장 둥근 모양을 포함하여 이러한 차원의 모든 단일 모양이 무한히 많은 닫힌 최소 표면을 가지고 있음을 증명 하여 또 다른 수십 년 된 추측을 해결했습니다. 밀도와 균등 분포가이 더 넓은 설정으로 이어질지, 최소값 이론의 어느 부분이 콤팩트하지 않은 매니 폴드와 차원이 8 이상인 매니 폴드 ( 새 논문이 이미 약간의 진전이있었습니다). 수학자들은 이러한 질문들 중 많은 부분이 늦어지기보다는 더 빨리 대답 될 것이라고 예측합니다. Neves는“상황이 매우 빠르게 진행되고 있습니다. "이제 매주 [과학적 사전 인쇄 사이트] arxiv를 봅니다. 누군가 방금 다른 문제를 해결했습니다." 관련 : 추상 표면의 끈질긴 탐험가 복잡한 시스템에 대한 단서를 제공하는 3 차원 프랙탈 과학자들은 편평함으로부터 곡선을 만들어 낸다 한 관점에서이 작업은 거의 40 년 동안 미완성으로 얽혀있는 이야기의 끝 (또는 끝에 가까움)을 표시합니다. 그러나 그것은 또한 새로운 시작입니다. 수학자들은 최소한의 표면에 대한 이러한 새로운 통찰이 그들이 사는 공간에 대해 우리에게 말해 줄 수있는 것을 이해하기 시작했습니다. Schoen은 "다른 극적인 응용 프로그램이 나올 것이라고 생각하지만 현재로서는 정확히 무엇을 말할 수 없습니다."라고 말했습니다. "기하학의 주요 방향이 될 것입니다."
편집자 주 : André Neves는 2018 년에 Simons Investigator로 지명되었습니다. Simons Foundation은 또한이 편집 독립 잡지에 자금을 지원합니다 .
.음, 꼬리가 보인다
.Plants can be larks or night owls just like us
식물은 우리처럼 종달새 족이나 올빼미 족이 될 수 있습니다

에 의해 Earlham 연구소 Dr. Hannah Rees, 영국 Earlham Institute의 박사후 연구원. 크레딧 : Earlham Institute DECEMBER 19, 2020
식물의 일주기 리듬을 지배하는 유전자를 탐구하는 새로운 연구에 따르면 식물은 인간에서 발견되는 것과 동일한 신체 시계의 변형을 가지고 있습니다. 이 연구는 DNA 코드의 단일 문자 변경이 잠재적으로 식물이 종달새인지 올빼미인지 결정할 수 있음을 보여줍니다.
이 발견은 농부와 작물 육종가가 자신의 위치에 가장 적합한 시계가있는 식물 을 선택하는 데 도움이 될 수 있으며, 수확량 을 높이고 기후 변화 를 견딜 수있는 능력까지도 높일 수 있습니다 . circadian 시계는 낮과 밤을 통해 유기체를 안내하는 분자 메트로놈입니다. 아침이 오면 cockadoodledooing하고 밤에는 커튼을 닫습니다. 식물에서는 새벽 광합성을 프라이밍하는 것부터 개화시기를 조절하는 것까지 다양한 과정을 조절합니다. 이러한 리드미컬 한 패턴은 지리, 위도, 기후 및 계절에 따라 달라질 수 있습니다. 식물 시계는 지역 조건에 가장 잘 대처할 수 있어야합니다.
Earlham Institute와 Norwich에있는 John Innes Center의 연구원들은 기후 변화에 대한 긴급한 위협 인 환경의 지역적 변화에 더 탄력적 인 작물을 재배하는 궁극적 인 목표를 가지고 자연적으로 얼마나 많은 일주기 변화가 존재하는지 더 잘 이해하기를 원했습니다. 이러한 지역적 차이의 유전 적 기초를 조사하기 위해 연구팀 은 스웨덴 애기 장대 식물의 다양한 일주기 리듬 을 조사 하여 시계의 변화하는 진드기와 관련된 유전자를 확인하고 검증했습니다.
Earlham Institute의 박사후 연구원이자이 논문의 저자 인 Hannah Rees 박사는 다음과 같이 말했습니다. "식물의 전체적인 건강 상태는 일주기 시계가 하루의 길이와 계절의 경과에 얼마나 가깝게 동기화되는지에 따라 크게 영향을받습니다. 신체 시계는 경쟁자, 포식자 및 병원균보다 우위를 점할 수 있습니다. "우리는 일광 시간과 기후에 극심한 변화를 경험하는 스웨덴에서 식물 생체 시계가 어떻게 영향을 받는지보고 싶었습니다. 신체 시계의 변화와 적응 뒤에있는 유전학을 이해하면 다른 지역에서 기후에 강한 작물을 더 많이 번식시킬 수 있습니다. " 연구팀은 스웨덴 전체에서 얻은 191 종의 애기 장대에서 유전자를 연구했다. 그들은 일주기 기능의 차이를 설명 할 수있는이 식물들 사이의 작은 유전자 차이를 찾고있었습니다.
그들의 분석에 따르면 특정 유전자 (COR28)의 단일 DNA 염기쌍 변화는 늦게 꽃이 피고 기간이 더 긴 식물에서 발견 될 가능성이 더 높습니다. COR28은 개화 시간, 동결 내성 및 일주기 시계 의 알려진 조정자입니다 . 모두 스웨덴의 현지 적응에 영향을 미칠 수 있습니다. Rees 박사는 "단일 유전자의 서열 내에서 단 하나의 염기쌍 변화가 시계가 똑딱 거리는 속도에 영향을 미칠 수 있다는 것은 놀랍습니다."라고 설명했습니다. 과학자들은 또한 선구적인 지연 형광 이미징 방법을 사용하여 일주기 시계가 다르게 조정 된 식물을 선별했습니다. 그들은 가장 이른 라이저와 최신 단계적 공장의 시계 사이에 10 시간 이상의 차이가 있음을 보여주었습니다. 이는 반대로 교대 패턴으로 작동하는 공장과 비슷합니다. 식물의 지리와 유전 적 조상 모두 영향을 미치는 것으로 보입니다. "Arabidopsis thaliana는 모델 식물 시스템"이라고 Rees 박사는 말했습니다. "지놈 염기 서열을 분석 한 최초의 식물이며 일주기 생물학에서 광범위하게 연구되었지만, 다른 시계 유형을 담당하는 유전자를 찾기 위해 이러한 유형의 연관 연구를 수행 한 사람은 이번이 처음입니다. "우리의 연구 결과 는 작물 육종가의 표적을 제시 하고 미래 연구를위한 플랫폼을 제공 할 수있는 몇 가지 흥미로운 유전자 를 강조합니다 . 당사의 지연 형광 이미징 시스템은 모든 녹색 광합성 물질에 사용할 수 있으므로 다양한 식물에 적용 할 수 있습니다. 다음 단계 이러한 발견을 브라 시카와 밀을 포함한 주요 농작물에 적용 할 것입니다. " 연구 결과는 Plant, Cell and Environment 저널에 게재되었습니다 .

더 알아보기 생물학적 시계와 추가 유전자 쌍은 중요한 식물 기능을 제어합니다. 추가 정보 : Hannah Rees et al, 스웨덴 애기 장대 접근에서 시계 유전자 좌위와 관련된 자연 발생 일주기 리듬 변이, 식물, 세포 및 환경 (2020). DOI : 10.1111 / pce.13941 Earlham Institute 제공
https://phys.org/news/2020-12-larks-night-owls.html
.Senescent tumor cells building three-dimensional tumor clusters
3 차원 종양 클러스터를 구축하는 노화 종양 세포

논문저자 이현규1, 논문저자 고려대 이현규 Hyun-Gyu Lee1,
June Hoan Kim 2, Woong Sun 2, Sung-Gil Chi3, WonshikChoi 1,4 & Kyoung J. Lee1 ,Scientific Reports volume 8 , 문서 번호 : 10503 ( 2018 ) | 인용문 다운로드 추상 세포 노화 (영구적 인 세포주기 정지)는 생물학적 유기체에 대한 유익한 중요성이 아직 탐구되기 시작한 공통적 인 흥미로운 현상입니다. 다른 한편으로는, 노화 세포는 그들 주위의 조직 구조를 변형시킬 수있다. 무한히 증식 할 수있는 능력을 가진 종양 세포는 그 현상으로부터 자유롭지 못합니다. 여기에 우리는 유방암 식민지의 고밀도 단일 층에있는 노화 세포가 주변에있는 비 노화 세포의 집합 센터 역할을하는 놀라운 관찰을보고합니다. 결과적으로, 노화 세포는 융합 성인 2D 종양 층에서 국소화 된 3D 세포 - 클러스터를 활발히 형성한다. 놀라운 현상을 뒷받침하는 생물 리 학적 메커니즘은 주로 유사 분열 세포 반올림, 동적 및 차동 세포 부착 및 세포 주 화성을 포함한다. 이러한 몇 가지 생물 물리학 적 요소를 통합함으로써 우리는 세포 Potts 모델을 통해 실험 관측을 재현 할 수있었습니다.
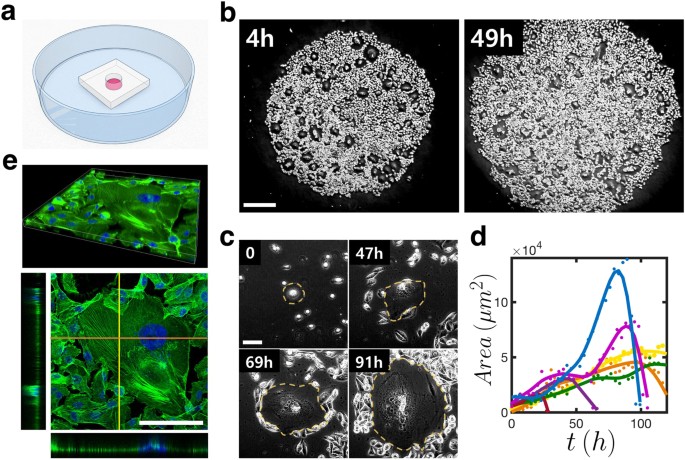
소개
세포 노화는 증식하는 세포가 완전한 성장 억제에 들어가고 그 체적을 극적으로 팽창시키는 (일반적으로, 2 차원 기질에서 튀긴 알 의 형태로) 생물체에서 공통적 인 현상이다 . 이 세포 상태의 근원은 강하게 연구되어왔다. 그러나 그 기본 메커니즘은 명확하지 않다. 1 , 2. 중요하게 노화 세포는 노화 관련 분비 표현형 (SASPs)으로 총체적으로 분류되는 다수의 분비물을 통해 그 이웃과 상호 작용한다. 이러한 분비 표현형은 생물에 부정적인 영향을 미치는 다양한 생물학적 과정에 관여하는 것으로 알려져있다. 예를 들어, 주위의 악성 종양 세포의 성장을 자극하는 친 염증성 사이토 카인과 케모카인이 그 중 3 개 , 4 개 입니다. 노화 세포의 축적은 또한 나이 - 관련 질환과 같은 더 많은 유기체 레벨 부작용과 연관된 5. 특히 조직 개조를 촉진 할 수도 있습니다. 예를 들어, 일부 세포 노화 따라서 암세포의 침윤 촉진 소프 주변 조직 구조를 만드는 세포 외 매트릭스 저하 프로테아제를 분비 6 , 7 , 8 . 한편, 노화 세포에 대한 유익한 효과에 대해서도 최근 논의된다. SASP는 배아 패터닝 9 , 10 및 상처 치료 11에 기여하는 단백질을 포함 합니다. 그럼에도 불구하고 이러한 조직 재생 효과가 SASP에 의해 생물 물리학 적으로 조율되는 방법의 정확한 성격은 특히 조직에 대한 개별 세포의 규모에서 많이 연구되어야합니다. 이 논문에서는 단일 클론 세포주 인 MDA-MB-231 (널리 사용되는 악성 유방암 세포주)의 시험 관내 배양을 바탕으로 초기 시딩 및 이웃 노화 방지와의 상호 작용에서 신생 세포의 출현을 신중하게 분석합니다 세포. 놀랍게도, 불멸화 된 종양 세포조차도 노화를 일으키는 것으로 나타났습니다 12 . 더 흥미 진진한 것은 노화 된 MDA-MB-231 세포가 인접한 종양 세포에 대한 인력의 중심 역할을하여 처음에 2 층 (2D) 콜로니의 단층에서 3 차원 (3D ) 세포 클러스터. 우리는 전환 이 시험 관내 에서 명확한 것으로 나타남을 본다.예를 들어 노화 세포가 조직 개질에 관여 할 수있는 사례. 또한 몇 가지 필수 메커니즘만으로 통합 된 컴퓨터 모델을 통한 관찰에 대한 경험적 설명을 제공합니다. Metropolis kinetics에서 작동하는 셀룰러 Potts 모델 (CPM)은 세포 부피의 보존, 유사 분열 세포 반올림 (결과적으로 세포 - 환경 유착의 동적 강도)과 같은 생물 물리학 적 과정을 재현하는 것을 목표로하며, 세포의 주 화성 운동. 실험 결과 MDA-MB-231 세포 배양 물 (처음에는 직경 2mm의 디스크 영역에 균일하게 도금 된 합류 단일 층 (confluent mono layer),도 1a 참조, 방법에 대한 자세한 내용 참조)은 다수의 노화 세포가 전체 집단으로 무작위로 출현한다 시간이 지남에 따라 증가한다 (그림 1b ). 그들은 '튀긴 계란'형태로 쉽게 식별 할 수 있습니다 (그림 1c ). 노화 된 상태로 들어가는 세포의 몸체는 꽤 합류하는 인구 내에서도 거대한 지역을 차지하기 위해 며칠 동안 측면으로 팽창합니다 (그림 1c ). 완전히 개발 노화 세포의 점유 면적이 현저하게 다른 하나에서 다를 수 있지만, 일반적으로 1.4 × 10 종종 크고 매우 큰 수 5 μ m (2) (도. 참조 1D를) - 전형적인 비 노화 세포보다 약 3 배 더 크다. 반면에 노화 세포의 몸은 ~ 2 μ m 만큼 얇 습니다 (그림 1e 의 두 측면보기 참조 ). 신체는 f-actin의 조밀 한 네트워크에 의해 구조적으로 잘 유지됩니다 (그림 1e 의 상단 그림 참조 ). 세포가 갑자기 파열되어 대사 과정을 끝낼 때까지 끊임없는 시공간 파동이 몸 전체에 나타나며 핵쪽으로 향하게됩니다.
https://www.nature.com/articles/s41598-018-28963-0
https://www.nature.com/articles/s41598-018-28963-0.pdf
https://html-online.com/editor/
.나의 oms 스토리텔링 노트 정리 중...
나는 오랜동안 서성거린 삶의 언저리에 있었다. 사람들 틈에서 늘 평범하게 살아왔다. 추운 겨울날에 마른 나뭇가지 사이로 비추는 자연의 밝은 빛줄기는 내게 정겨움을 주었으나 늘 거리의 간판 불빛 아래에 비에 젖은 밤 도시의 길을 걷곤 하였다.
내 젊은 날, 결혼 전에는 대학가 와인 하우스 카페에서 마티니를 즐기며 연인을 바라보곤 하였다. 추억은 오랜 시간 느리게 기억에서 희미해져 갔다. 세상은 어디에서 와서 가든지 기억에 머물지 않는 한 사라지거나 처음부터 없던 것들 처럼 보일 것이다. 이제는 이여져 있는 것처럼 느낀다. 삶이나 주검이나 지구의 이세상이나 외계의 저세상이나 연결된듯 하다.
210124 주요 메모
드디어 모든 것을 통합하며 설명하는 것이 가능한 oms 스토리텔링을 찾았다. 과학적 의문에 해답을 oms에서 찾은 결과 종교가 말하는 영생불멸과 철학이 말하는 진리와 진화론과 카오스이론이 말하는 복잡하고 심오한 세계를 설명하는 수준에 이르렀다. 하지만 금새 어떤 일이 기적처럼 나타날 일은 아니다. 우리가 빅뱅사건과 태양계에서 벌어지는 일들이 금새 감지할 수준이 아니라는 점 때문이며 나의 우주통달 감지력은 oms을 탐색하는 경로가 세상사 관심뿐인 일반이들과 다른 감지경로 때문에 가능했다. 우주만물이 보이는 경로가 있음이다.
1.마방진으로 바라본 세상사는 전체적으로 조화와 질서 그리고 균형을 이룬다.
2. 마방진 내부에 우주 전체의 물질을 개체화 시킨 단위로 세상사 자연현상이 전체적으로 매직섬을 이룬다.
3. 그 소립자로 부터 항성에 이르는 우리우주의 개체들은 다중우주 전체에 참여된 존재이다.
4.마방진은 oms의 단위를 가졌고 oms는 아인쉬타인의 질량에너지 등가원리를 증명한다.
4. oms내에 1의 값은 물질의 최소단위이고 그물질로 인체도 만들어 영혼의 빛을 나타내며 우주를 지적으로 드려다 볼 수 있다.
5. 인체는 oms의 스몰러들의 정적 동적인 순간적 무한대 여행으로 생겨난 물질간에 잠시 모여서 생긴 것이다.
210125
6.빅뱅으로 부터 출현된 우주가 작은 구체에서 극단적으로 커지는 구체의 표면을 가진다면 그것은 사각형 mser나 oms 안에서 사각형과 동기화하는 한계에 이른다. 고로 우주의 확장의 끝이 oms이다.
b0acfd0000e0 000ac0f00bde 0c0fab000e0d e00d0c0b0fa0 f000e0b0dac0 d0f000cae0b0 0b000f0ead0c 0deb00ac000f ced0ba00f000 a0b00e0dc0f0 0ace00df000b 0f00d0e0bc0a
댓글